题目内容
已知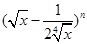 的展开式中,前三项系数的绝对值依次成等差数列.
的展开式中,前三项系数的绝对值依次成等差数列.
(Ⅰ)证明展开式中没有常数项;
(Ⅱ)求展开式中所有的有理项.
【答案】
(Ⅰ)见解析(Ⅱ) ,
,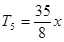 ,
,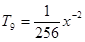
【解析】本试题主要是考查了二项式定理中通项公式的运用。
(1)先求解其通项公式,然后令x的次数为零,看是否成立说明结论。
(2)因为展开式中所有的有理项.即为未知数的次数为整数,那么可知满足题意的项有3项。
解 :由题意: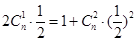 ,即
,即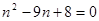 ,∴
,∴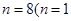 舍去)
舍去)
∴

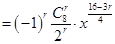
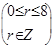
①若 是常数项,则
是常数项,则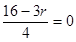 ,即
,即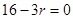 ,∵
,∵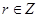 ,这不可能,∴展开式中没有常数项;
,这不可能,∴展开式中没有常数项;
②若 是有理项,当且仅当
是有理项,当且仅当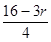 为整数,∴
为整数,∴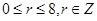 ,∴
,∴
 ,即
展开式中有三项有理项,分别是:
,即
展开式中有三项有理项,分别是: ,
,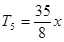 ,
,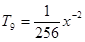 .
.

练习册系列答案
相关题目
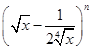 的展开式中,前三项系数的绝对值依次成等差数列。
的展开式中,前三项系数的绝对值依次成等差数列。 的展开式中,前三项系数的绝对值依次成等差数列。
的展开式中,前三项系数的绝对值依次成等差数列。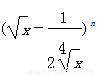 的展开式中,前三项系数的绝对值依次成等差数列.(1)求:展开式中各项系数的和;(2)求展开式中所有有理项.
的展开式中,前三项系数的绝对值依次成等差数列.(1)求:展开式中各项系数的和;(2)求展开式中所有有理项.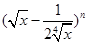 的展开式中,前三项的系数的绝对值依次成等差数列,
的展开式中,前三项的系数的绝对值依次成等差数列,