题目内容
某工厂为某工地生产容器为
π(米3)的无盖圆柱形容器,容器的底面半径为r(米),而且制造底面的材料每平方米为30元,制造容器的材料每平方米为20元,设计时材料的厚度可忽略不计.
(1)制造容器的成本y(元)表示成r的函数;
(2)工地要求容器的底面半径r∈[2,3](米),问如何设计容器的尺寸,使其成本最低?,最低成本是多少?(精确到元)
| 3 | 2 |
(1)制造容器的成本y(元)表示成r的函数;
(2)工地要求容器的底面半径r∈[2,3](米),问如何设计容器的尺寸,使其成本最低?,最低成本是多少?(精确到元)
分析:(1)由无盖圆锥形容器容积为
π米3,我们设底面半径为r,易求出底面面积,及侧(容器壁)面积,然后再根据制造底面的材料每平方米30元,制造容器壁的材料每平方米20元,我们可得到容器的成本y(元)表示为r的函数的解析式;
(2)根据(1)中的容器的成本y(元)表示为r的函数的解析式,结合函数的单调性,我们易求出成本最低值,及对应的底面半径r的值.
| 3 |
| 2 |
(2)根据(1)中的容器的成本y(元)表示为r的函数的解析式,结合函数的单调性,我们易求出成本最低值,及对应的底面半径r的值.
解答:解:(1)容器壁的高为h米,容器的体积为V米3.
由V=πr2h,得πr2h=
π.
∴h=
∴y=30•πrr2+20•2πrh=30πr2+
=30π(r2+
)(r>0)
(2)由y=30π(r2+
)=30π(r2+
+
)≥30π•3
=90π
当且仅当r2=
.即r=1时,取等号.
由1∉[2,3];下面研究函数Q(x)=r2+
在r∉[2,3]上的单调性.
设2≤r1<r2≤3,Q(r1)-Q(r2)=(r12+
)-(r22+
)=(
-
)+2(
-
)=(r1-r2)•
,
∵2≤r1<r2≤3,
∴(r1-r2)<0,
>0,
∴Q(r1)-Q(r2)<0,即Q(r)在[2,3]上为增函数.
当r=2时,y取得最小值150π≈465(元).
∴当r=2米,h=
米时,造价最低为465元.
由V=πr2h,得πr2h=
| 3 |
| 2 |
∴h=
| 3 |
| 2r2 |
∴y=30•πrr2+20•2πrh=30πr2+
| 60π |
| r |
| 2 |
| r |
(2)由y=30π(r2+
| 2 |
| r |
| 1 |
| r |
| 1 |
| r |
| 3 | r2•
| ||||
当且仅当r2=
| 1 |
| r |
由1∉[2,3];下面研究函数Q(x)=r2+
| 2 |
| r |
设2≤r1<r2≤3,Q(r1)-Q(r2)=(r12+
| 2 |
| r1 |
| 2 |
| r2 |
| r | 2 1 |
| r | 2 2 |
| 1 |
| r1 |
| 1 |
| r2 |
| r1+r2-2 |
| r1r2 |
∵2≤r1<r2≤3,
∴(r1-r2)<0,
| r1+r2-2 |
| r1r2 |
∴Q(r1)-Q(r2)<0,即Q(r)在[2,3]上为增函数.
当r=2时,y取得最小值150π≈465(元).
∴当r=2米,h=
| 3 |
| 8 |
点评:函数的实际应用题,我们要经过析题→建模→解模→还原四个过程,在建模时要注意实际情况对自变量x取值范围的限制,解模时也要实际问题实际考虑.将实际的最大(小)化问题,利用函数模型,转化为求函数的最大(小)是最优化问题中,最常见的思路之一.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
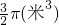 的无盖圆柱形容器,容器的底面半径为r(米),而且制造底面的材料每平方米为30元,制造容器的材料每平方米为20元,设计时材料的厚度可忽略不计.
的无盖圆柱形容器,容器的底面半径为r(米),而且制造底面的材料每平方米为30元,制造容器的材料每平方米为20元,设计时材料的厚度可忽略不计. 的无盖圆柱形容器,容器的底面半径为r(米),而且制造底面的材料每平方米为30元,制造容器的材料每平方米为20元,设计时材料的厚度可忽略不计.
的无盖圆柱形容器,容器的底面半径为r(米),而且制造底面的材料每平方米为30元,制造容器的材料每平方米为20元,设计时材料的厚度可忽略不计.