题目内容

数列{a_n}的各项均为正数，S_n为其前n项和，对于任意n∈N^*，总有a_n，S_n，a_n²成等差数列．设数列{b_n}的前n项和为T_n，且b_n= $数学公式$ ，则对任意实数x∈（1，e]（e是常数，e=2.71828…）和任意正整数n，T_n＜

A.
1
B.
2
C.
3
D.
4

B
分析：对任意实数x∈（1，e]和任意正整数n，总有b_n= $\text{[math]}$ ，然后用放缩法能够导出T_n＜2．
解答：∵对任意实数x∈（1，e]和任意正整数n，
总有b_n= $\text{[math]}$ ，
∴T_n≤ $\text{[math]}$ +…+ $\text{[math]}$ ＜1+ $\text{[math]}$ +…+ $\text{[math]}$
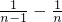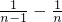=1+1- $\text{[math]}$ + $\text{[math]}$ +…+ $\text{[math]}$ =2- $\text{[math]}$ ＜2．
故选B．
点评：本题考查数列的应用，解题时要注意放绾法的合理运用．

练习册系列答案

导学案快乐学习系列答案

孟建平各地期末试卷精选系列答案

名师三导学练考系列答案

轻松小卷系列答案

提分百分百检测卷系列答案

权威考卷系列答案

密码大考卷系列答案

宝贝计划期末冲刺夺100分系列答案

能考试全能100分系列答案

名师名校全能金卷系列答案

相关题目

数列{a_n}的各项均为正数，S_n为其前n项和，对于任意n∈N*，总有2S_n=a_n²+a_n．
（1）求数列{a_n}的通项公式；
（2）设正数数列{c_n}满足a_n+1=（c_n）ⁿ⁺¹，（n∈N^*），求数列{c_n}中的最大项；

设数列{a_n}的各项均为正数，它的前n项和为S_n（n∈N*），已知点（a_n，4S_n）在函数f （x）=x²+2x+1的图象上．
（1）证明{a_n}是等差数列，并求a_n；
（2）设m、k、p∈N*，m+p=2k，求证：

；
（3）对于（2）中的命题，对一般的各项均为正数的等差数列还成立吗？如果成立，请证明你的结论，如果不成立，请说明理由．

数列{a_n}的各项均为正数，S_n为其前n项和，对于任意n∈N^*，总有a_n、S_n、（a_n）²成等差数列．
（I）求数列{a_n}的通项公式；
（II）设bn=an(

)n，数列{b_n}的前n项和是T_n，求证：

若数列{a_n}的前n项和为S_n，则下列命题：
（1）若数列{a_n}是递增数列，则数列{S_n}也是递增数列；
（2）数列{S_n}是递增数列的充要条件是数列{a_n}的各项均为正数；
（3）若{a_n}是等差数列（公差d≠0），则S₁•S₂…S_k=0的充要条件是a₁•a₂…a_k=0．
（4）若{a_n}是等比数列，则S₁•S₂…S_k=0（k≥2，k∈N）的充要条件是a_n+a_n+1=0．
其中，正确命题的个数是（　　）

（2012•奉贤区二模）数列{a_n} 的各项均为正数，a₁=p，p＞0，k∈N^*，a_n+a_n+k=f（p，k）•pⁿ．
（1）当k=1，f（p，k）=p+k，p=5时，求a₂，a₃；
（2）若数列{a_n}成等比数列，请写出f（p，k）满足的一个条件，并写出相应的通项公式（不必证明）；
（3）当k=1，f（p，k）=p+k时，设T_n=a₁+2a₂+3a₃+…+2a_n+a_n+1，求T_n．