题目内容
已知向量![]() ,(其中实数
,(其中实数![]() 和
和![]() 不同时为零),当
不同时为零),当![]() 时,有
时,有![]() ,当
,当![]() 时,
时,![]() .
.
(1) 求函数式![]() ;(2)求函数
;(2)求函数![]() 的单调递减区间;
的单调递减区间;
(3)若对![]()
![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
解:(1)当![]() 时,由
时,由![]()
得![]() ,
,
![]() ;(
;(![]() 且
且![]() )------------------------------------2分
)------------------------------------2分
当![]() 时,由
时,由![]() .
.
得![]() --------------------------------------4分
--------------------------------------4分
∴  ---------------------5分
---------------------5分
(2)当![]() 且
且![]() 时, 由
时, 由![]() <0,
<0,
解得![]() ,----------------6分
,----------------6分
当![]() 时,
时,
![]() ------------------------------8分
------------------------------8分
∴函数![]() 的单调减区间为(-1,0)和(0,1) -------------9分
的单调减区间为(-1,0)和(0,1) -------------9分
(3)对![]()
![]() ,
,
都有![]()
即![]() ,
,
也就是![]()
对![]()
![]() 恒成立,----------------------------------11分
恒成立,----------------------------------11分
由(2)知当![]() 时,
时,
![]() ∴ 函数
∴ 函数![]() 在
在![]() 和
和![]() 都单调递增----------------------12分
都单调递增----------------------12分
又![]() ,
,![]()
当![]() 时
时
![]() ,
,
∴当![]() 时,
时,
![]()
同理可得,当![]() 时,
时,
有![]() ,
,
综上所述得,
对![]()
![]() ,
,
![]() 取得最大值2;
取得最大值2;
∴ 实数![]() 的取值范围为
的取值范围为![]() .----------------------14分
.----------------------14分

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 ,(其中实数
,(其中实数 和
和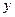 不同时为零),当
不同时为零),当 时,有
时,有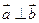 ,当
,当 时,
时, .
. ;
; 的单调递减区间;
的单调递减区间; ,都有
,都有 ,求实数
,求实数 的取值范围.
的取值范围.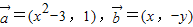 ,(其中实数y和x不同时为零),当|x|<2时,有
,(其中实数y和x不同时为零),当|x|<2时,有 ,当|x|≥2时,
,当|x|≥2时, .
. ,(其中实数y和x不同时为零),当|x|<2时,有
,(其中实数y和x不同时为零),当|x|<2时,有 ,当|x|≥2时,
,当|x|≥2时, .
. ,(其中实数y和x不同时为零),当|x|<2时,有
,(其中实数y和x不同时为零),当|x|<2时,有 ,当|x|≥2时,
,当|x|≥2时, .
.