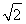题目内容
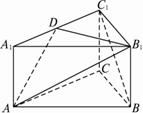
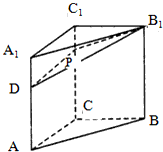 如图所示,三棱柱ABC-A1B1C1的侧棱长为3,底面边长A1C1=B1C1=1,且∠A1C1B1=90°,D点在棱AA1上且AD=2DA1,P点在棱C1C上,则
如图所示,三棱柱ABC-A1B1C1的侧棱长为3,底面边长A1C1=B1C1=1,且∠A1C1B1=90°,D点在棱AA1上且AD=2DA1,P点在棱C1C上,则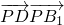 的最小值为
的最小值为
- A.

- B.

- C.

- D.

B
分析:建立如图所示的直角坐标系,设P(0,0,z),求出 和
和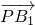 的坐标,求出
的坐标,求出  •
•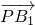 =
= +
+ ,利用二次函数的性质求出它的最小值.
,利用二次函数的性质求出它的最小值.
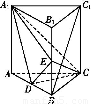
解答: 解:建立如图所示的直角坐标系,则D(1,0,2),B1(0,1,3),设P(0,0,z),
解:建立如图所示的直角坐标系,则D(1,0,2),B1(0,1,3),设P(0,0,z),
则 =(1,0,2-z),
=(1,0,2-z),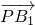 =(0,1,3-z),
=(0,1,3-z),
∴ •
•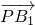 =0+0+(2-z)(3-z)=
=0+0+(2-z)(3-z)= +
+ ,故当z=
,故当z= 时,
时, •
•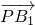 取得最小值为-
取得最小值为- ,
,
故选B.
点评:本题主要考查两个向量的数量积的定义,两个向量坐标形式的运算,属于基础题.
分析:建立如图所示的直角坐标系,设P(0,0,z),求出
 和
和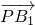 的坐标,求出
的坐标,求出  •
•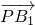 =
= +
+ ,利用二次函数的性质求出它的最小值.
,利用二次函数的性质求出它的最小值.解答:
 解:建立如图所示的直角坐标系,则D(1,0,2),B1(0,1,3),设P(0,0,z),
解:建立如图所示的直角坐标系,则D(1,0,2),B1(0,1,3),设P(0,0,z),则
 =(1,0,2-z),
=(1,0,2-z),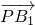 =(0,1,3-z),
=(0,1,3-z),∴
 •
•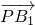 =0+0+(2-z)(3-z)=
=0+0+(2-z)(3-z)= +
+ ,故当z=
,故当z= 时,
时, •
•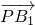 取得最小值为-
取得最小值为- ,
,故选B.
点评:本题主要考查两个向量的数量积的定义,两个向量坐标形式的运算,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,在边长为12的正方形ADD1A1中,点B,C在线段AD上,且AB=3,BC=4,作BB1∥AA1,分别交A1D1、AD1于点B1、P,作CC1∥AA1,分别交A1D1、AD1于点C1、Q,将该正方形沿BB1、CC1折叠,使得DD1与AA1重合,构成如图所示的三棱柱ABC-A1B1C1.
如图所示,在边长为12的正方形ADD1A1中,点B,C在线段AD上,且AB=3,BC=4,作BB1∥AA1,分别交A1D1、AD1于点B1、P,作CC1∥AA1,分别交A1D1、AD1于点C1、Q,将该正方形沿BB1、CC1折叠,使得DD1与AA1重合,构成如图所示的三棱柱ABC-A1B1C1. (2012•淮北一模)如图所示,三棱柱ABC-A1B1Cl中,AB=AC=AA1=2,面ABC1⊥面AAlClC,∠AAlCl=∠BAC1=600,
(2012•淮北一模)如图所示,三棱柱ABC-A1B1Cl中,AB=AC=AA1=2,面ABC1⊥面AAlClC,∠AAlCl=∠BAC1=600,