题目内容
(本小题满分14分)在平面直角坐标系 中,已知直线
中,已知直线 被圆
被圆 截得的弦长为
截得的弦长为 .
.
(Ⅰ)求圆 的方程;
的方程;
(Ⅱ)设圆 和
和 轴相交于A,B两点,点P为圆
轴相交于A,B两点,点P为圆 上不同于A,B的任意一点,直线
上不同于A,B的任意一点,直线 ,
, 交
交 轴于M,N两点.当点P变化时,以
轴于M,N两点.当点P变化时,以 为直径的圆
为直径的圆 是否经过圆
是否经过圆 内一定点?请证明你的结论.
内一定点?请证明你的结论.
 中,已知直线
中,已知直线 被圆
被圆 截得的弦长为
截得的弦长为 .
.(Ⅰ)求圆
 的方程;
的方程;(Ⅱ)设圆
 和
和 轴相交于A,B两点,点P为圆
轴相交于A,B两点,点P为圆 上不同于A,B的任意一点,直线
上不同于A,B的任意一点,直线 ,
, 交
交 轴于M,N两点.当点P变化时,以
轴于M,N两点.当点P变化时,以 为直径的圆
为直径的圆 是否经过圆
是否经过圆 内一定点?请证明你的结论.
内一定点?请证明你的结论.(Ⅰ)圆 的方程为
的方程为
(Ⅱ)当点P变化时,以 为直径的圆
为直径的圆 经过圆
经过圆 内一定点
内一定点 。
。
 的方程为
的方程为
(Ⅱ)当点P变化时,以
 为直径的圆
为直径的圆 经过圆
经过圆 内一定点
内一定点 。
。(1)由 得
得
所以圆心 ,所以圆心到直线
,所以圆心到直线 的距离为
的距离为


所以圆 的方程为
的方程为
(2)由(1)可知 ,
,
由题意可知直线PA的斜率存在且不为零,可设为
所以直线PA的方程为 ,令x=0得y=6k,
,令x=0得y=6k,
因为 ,所以直线PB的方程为
,所以直线PB的方程为 ,令x=0得y=
,令x=0得y= ,
,
所以MN的中点 ,不妨设
,不妨设 ,则
,则
所以以M,N为直径的圆方程为
化简得 ,即
,即
令 ,解得
,解得
经检验 不在圆
不在圆 内,
内, 在圆
在圆 内
内
所以当点P变化时,以 为直径的圆
为直径的圆 经过圆
经过圆 内一定点
内一定点 。
。
 得
得
所以圆心
 ,所以圆心到直线
,所以圆心到直线 的距离为
的距离为


所以圆
 的方程为
的方程为
(2)由(1)可知
 ,
,
由题意可知直线PA的斜率存在且不为零,可设为

所以直线PA的方程为
 ,令x=0得y=6k,
,令x=0得y=6k,
因为
 ,所以直线PB的方程为
,所以直线PB的方程为 ,令x=0得y=
,令x=0得y= ,
,
所以MN的中点
 ,不妨设
,不妨设 ,则
,则
所以以M,N为直径的圆方程为

化简得
 ,即
,即
令
 ,解得
,解得
经检验
 不在圆
不在圆 内,
内, 在圆
在圆 内
内所以当点P变化时,以
 为直径的圆
为直径的圆 经过圆
经过圆 内一定点
内一定点 。
。
练习册系列答案
相关题目
 ,求EF的长。
,求EF的长。
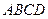 内,两个圆
内,两个圆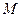 、
、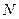 分别与矩形两边相切,且两圆互相外切。若矩形的长和宽分别为
分别与矩形两边相切,且两圆互相外切。若矩形的长和宽分别为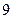 和
和 ,试把两个圆的面积之和
,试把两个圆的面积之和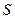 表示为圆
表示为圆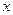 的函数关系式,并求
的函数关系式,并求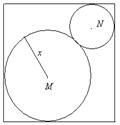
 x+y-2
x+y-2 =4得的劣弧所对的圆心角为
=4得的劣弧所对的圆心角为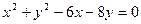 ,设该圆过点
,设该圆过点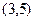 的最长弦和最短弦分别为
的最长弦和最短弦分别为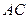 和
和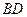 ,则四边形
,则四边形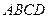 的面积为 ( )
的面积为 ( )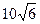
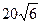
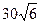
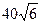
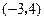 为圆心,且与
为圆心,且与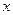 轴相切的圆的方程是( )
轴相切的圆的方程是( )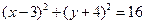

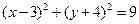
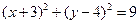
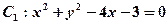 和
和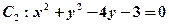 的交点的圆方程
的交点的圆方程
 表示的曲线是( )
表示的曲线是( ) 为a,b的调和平均数。如图,C为线段AB上的点,且AC=a,CB=b,O为AB中点,以AB为直径做半圆。过点C作AB的垂线交半圆于D。连结OD,AD,BD。过点C作OD的垂线,垂足为E。则图中线段OD的长度是a,b的算术平均数,线段 的长度是a,b的几何平均数,线段 的长度是a,b的调和平均数。
为a,b的调和平均数。如图,C为线段AB上的点,且AC=a,CB=b,O为AB中点,以AB为直径做半圆。过点C作AB的垂线交半圆于D。连结OD,AD,BD。过点C作OD的垂线,垂足为E。则图中线段OD的长度是a,b的算术平均数,线段 的长度是a,b的几何平均数,线段 的长度是a,b的调和平均数。