题目内容
【题目】某学校的平面示意图为如下图五边形区域![]() ,其中三角形区域
,其中三角形区域![]() 为生活区,四边形区域
为生活区,四边形区域![]() 为教学区,
为教学区, ![]() 为学校的主要道路(不考虑宽度).
为学校的主要道路(不考虑宽度). ![]() .
.
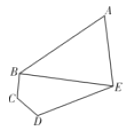
(1)求道路![]() 的长度;(2)求生活区
的长度;(2)求生活区![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)连接BD,由余弦定理可得BD,由已知可求![]() ,
, ![]() ,可得
,可得![]() ,利用勾股定理即可得解
,利用勾股定理即可得解![]() 的值. (2)设
的值. (2)设![]() ,由正弦定理,可得
,由正弦定理,可得![]() ,利用三角函数恒等变换的应用化简可得
,利用三角函数恒等变换的应用化简可得![]() ,结合范围3
,结合范围3![]() ,利用正弦函数的性质可求
,利用正弦函数的性质可求![]() 面积的最大值,从而得解.
面积的最大值,从而得解.
试题解析:
(1)
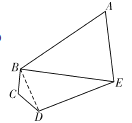
如图,连接![]() ,在
,在![]() 中,由余弦定理得:
中,由余弦定理得:
![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴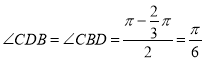 ,
,
又![]() ,∴
,∴![]() .
.
在![]() 中,所以
中,所以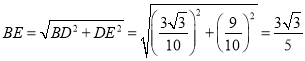 .
.
(2)设![]() ,∵
,∵![]() ,∴
,∴![]() .
.
在![]() 中,由正弦定理,得
中,由正弦定理,得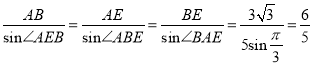 ,
,
∴![]() .
.
∴![]()
![]() .
.
∵![]() ,∴
,∴![]() .
.
∴当![]() ,即
,即![]() 时,
时, ![]() 取得最大值为
取得最大值为![]() ,
,
即生活区![]() 面积的最大值为
面积的最大值为![]() .
.
注:第(2)问也可用余弦定理和均值不等式求解.

练习册系列答案
相关题目




