题目内容
下列命题:
①△ABC中,若A<B,则cos2A<cos2B;
②若A,B,C为△ABC的三个内角,则
+
的最小值为
③已知an=sin
+
(n∈N*),则数列{an}中的最小项为
;
④若函数f(x)=log2(x+1),且0<a<b<c,则
<
<
;
⑤函数f(x)=
+
的最小值为
.
其中所有正确命题的序号是
①△ABC中,若A<B,则cos2A<cos2B;
②若A,B,C为△ABC的三个内角,则
| 4 |
| A |
| 1 |
| B+C |
| 9 |
| π |
③已知an=sin
| nπ |
| 6 |
| 16 | ||
2+sin
|
| 19 |
| 3 |
④若函数f(x)=log2(x+1),且0<a<b<c,则
| f(a) |
| a |
| f(b) |
| b |
| f(c) |
| c |
⑤函数f(x)=
| x2-2x+5 |
| x2-4x+13 |
| 29 |
其中所有正确命题的序号是
②③
②③
.分析:①先有正弦定理判断出sinA与sinB的大小关系,然后再利用余弦的倍角公式展开进行化简讨论.
②先利用A+B+C=π,进行化简,然后利用基本不等式进行证明.
③将数列转化为基本不等式的形式,然后利用基本不等式进行判断.
④构造函数
,转化为斜率的大小进行判断.
⑤先配方,将根式转化为两点间距离之和的最小值来求.
②先利用A+B+C=π,进行化简,然后利用基本不等式进行证明.
③将数列转化为基本不等式的形式,然后利用基本不等式进行判断.
④构造函数
| f(x) |
| x |
⑤先配方,将根式转化为两点间距离之和的最小值来求.
解答:
 解:①①△ABC中,若A<B,则a<b,由正弦定理
解:①①△ABC中,若A<B,则a<b,由正弦定理
=
得0<sinA<sinB,又cos?2A=1-2sin?2A,cos?2B=1-2sin?2B,所以cos2A>cos2B,所以①错误.
②因为A+B+C=π,α=A,β=B+C,α+β=π,所以
=1,原式等价为
+
=(
+
)?1=(
+
)(
)=
(5+
+
)≥
(5+2
)=
,当且仅当
=
,即α=2β时取等号.所以②正确.
③因为an=sin
+
=2+sin?
+
-2,因为1≤2+sin?
≤3,所以设t=2+sin?
,则1≤t≤3.因为函数y=t+
-2在区间(0,4)上单调递减,所以在[1,3]上单调递减,所以当t=3时,函数有最小值3+
-2=
,则对应数列{an}中的最小项为
,所以③正确.
④令g(x)=
,则函数g(x)的几何意义为曲线上点与原点连线斜率的大小.由题意可知
,
,
分别看作函数f(x)=log2(x+1)图象上的点(a,f(a)),(b,f(b)),(c,f(b))与原点连线的斜率,由图象可知
>
>
,所以④错误.
⑤原式可化简为f(x)=
+
=
+
,设点P(x,0),A(1,2),B(2,3),
则原式等价为|PA|+|PB|的最小值,找出点A关于x轴的对称点D(1,-2).则|PA|+|PB|=|PD|+|PB|≥|PD|,所以最小值为|PD|=
=
=
.所以⑤错误.
所有正确命题的序号是②③.
故答案为:②③.

 解:①①△ABC中,若A<B,则a<b,由正弦定理
解:①①△ABC中,若A<B,则a<b,由正弦定理| a |
| sin?A |
| b |
| sin?B |
②因为A+B+C=π,α=A,β=B+C,α+β=π,所以
| α+β |
| π |
| 4 |
| α |
| 1 |
| β |
| 4 |
| α |
| 1 |
| β |
| 4 |
| α |
| 1 |
| β |
| α+β |
| π |
| 1 |
| π |
| α |
| β |
| 4β |
| α |
| 1 |
| π |
|
| 9 |
| π |
| α |
| β |
| 4β |
| α |
③因为an=sin
| nπ |
| 6 |
| 16 | ||
2+sin
|
| nπ |
| 6 |
| 16 | ||
2+sin?
|
| nπ |
| 6 |
| nπ |
| 6 |
| 16 |
| t |
| 16 |
| 3 |
| 19 |
| 3 |
| 19 |
| 3 |
④令g(x)=
| f(x) |
| x |
| f(a) |
| a |
| f(b) |
| b |
| f(c) |
| c |
| f(a) |
| a |
| f(b) |
| b |
| f(c) |
| c |
⑤原式可化简为f(x)=
| (x-1)2+4 |
| (x-2)2+9 |
| (x-1)2+(0-2)2 |
| (x-2)2+(0-3)2 |
则原式等价为|PA|+|PB|的最小值,找出点A关于x轴的对称点D(1,-2).则|PA|+|PB|=|PD|+|PB|≥|PD|,所以最小值为|PD|=
| (2-1)2+(-2-3)2 |
| 1+25 |
| 26 |
所有正确命题的序号是②③.
故答案为:②③.
点评:本题重点考查了基本不等式的应用,以及对复杂问题,要根据几何意义进行转化的数学思路.对学生的转化能力,运算能力都有很高的要求,这类问题的难度较大,综合性较强.

练习册系列答案
相关题目
 ,
, ;
; 是周期为2
是周期为2 的偶函数;
的偶函数; 的焦点为F,点P为抛物线上任意一点,则
的焦点为F,点P为抛物线上任意一点,则 的最小值为2;
的最小值为2;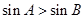 ;②若对一切
;②若对一切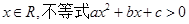 恒成立,则必有
恒成立,则必有 ;③不等式
;③不等式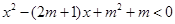 的解集为
的解集为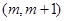 ;④函数
;④函数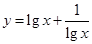 最小值为2,其中正确的序号为__________ 。
最小值为2,其中正确的序号为__________ 。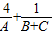 的最小值为
的最小值为
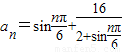 (n∈N*),则数列{an}中的最小项为
(n∈N*),则数列{an}中的最小项为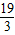 ;
;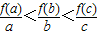 ;
;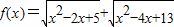 的最小值为
的最小值为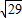 .
.