题目内容
已知梯形ABCD中,AD∥BC,∠ABC =∠BAD =![]() ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .
(1) 当x=2时,求证:BD⊥EG ;
(2) 若以F、B、C、D为顶点的三棱锥的体积记为f(x),求f(x)的最大值;
(3) 当 f(x)取得最大值时,求二面角D-BF-C的余弦值.
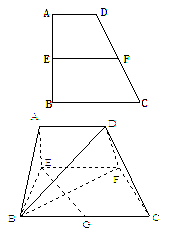
(2) ![]() (3)
(3) ![]()
解析:
)作DH⊥EF于H,连BH,GH,……………1分
由平面![]() 平面
平面![]() 知:DH⊥平面EBCF,
知:DH⊥平面EBCF,
而EG![]() 平面EBCF,故EG⊥DH。
平面EBCF,故EG⊥DH。
又四边形BGHE为正方形,∴EG⊥BH,
BH![]() DH=H,故EG⊥平面DBH,………………… 3分
DH=H,故EG⊥平面DBH,………………… 3分
而BD![]() 平面DBH,∴ EG⊥BD。………………… 4分
平面DBH,∴ EG⊥BD。………………… 4分
(或者直接利用三垂线定理得出结果)
(2)∵AD∥面BFC,
所以 ![]() VA-BFC=
VA-BFC=![]() =··4·(4-x)·x
=··4·(4-x)·x
![]() ………………………………………………………………………7分
………………………………………………………………………7分
即![]() 时
时![]() 有最大值为
有最大值为![]() 。…………………………………………………………8分
。…………………………………………………………8分
(3)(法一)设平面DBF的法向量为![]() ,∵AE=2, B(2,0,0),D(0,2,2),
,∵AE=2, B(2,0,0),D(0,2,2),
 F(0,3,0),∴
F(0,3,0),∴![]()
![]() (-2,2,2), ………………………………9分
(-2,2,2), ………………………………9分
则 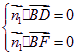 ,
,
即![]() ,
,![]()
取x=3,则y=2,z=1,∴![]()
面BCF的一个法向量为![]() ……………………………12分
……………………………12分
则cos<![]() >=
>= …………………………………………13分
…………………………………………13分
由于所求二面角D-BF-C的平面角为钝角,所以此二面角的余弦值为-![]() …………………14分
…………………14分

练习册系列答案
相关题目
 如图,已知梯形ABCD中|AB|=2|CD|,点E分有向线段
如图,已知梯形ABCD中|AB|=2|CD|,点E分有向线段
 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=
 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD= 已知梯形ABCD中,AD∥BC,
已知梯形ABCD中,AD∥BC, 如图,已知梯形ABCD中,AD∥BC,∠ABC=90°,AD=a,BC=2a,∠DCB=60°,在平面ABCD内,过C作l⊥CB,以l为轴将梯形ABCD旋转一周,求所得旋转体的表面积及体积.
如图,已知梯形ABCD中,AD∥BC,∠ABC=90°,AD=a,BC=2a,∠DCB=60°,在平面ABCD内,过C作l⊥CB,以l为轴将梯形ABCD旋转一周,求所得旋转体的表面积及体积.