题目内容
已知0<α<π,sinα+cosα=
,则cos2α的值为( )
| 1 |
| 2 |
A、
| ||||
B、-
| ||||
C、±
| ||||
D、-
|
分析:首先由已知条件与同角正余弦关系式列方程组,然后解sinα(因为0<α<π),最后由余弦的二倍角公式解之.
解答:解:∵
∴2sin2α-sinα -
=0
解得sinα=
,
又0<α<π,∴sinα=
.
∴cos2α=1-2sin2α=-
.
故选B.
|
∴2sin2α-sinα -
| 3 |
| 4 |
解得sinα=
1±
| ||
| 4 |
又0<α<π,∴sinα=
1+
| ||
| 4 |
∴cos2α=1-2sin2α=-
| ||
| 4 |
故选B.
点评:本题考查同角正余弦关系式、余弦的二倍角公式及方程思想.

练习册系列答案
相关题目
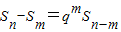 恒成立.
恒成立.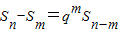 恒成立.
恒成立. 恒成立.
恒成立.