题目内容
(14分)已知数列![]() 中,
中,![]() (
(![]() 为常数),
为常数),![]() 是
是![]() 的前
的前![]() 项和,且
项和,且![]() 是
是![]() 与
与![]() 的等差中项。
的等差中项。
(1)求![]() ; (2)猜想
; (2)猜想![]() 的表达式,并用数学归纳法加以证明。
的表达式,并用数学归纳法加以证明。
解:(1)根据题意 ![]() …………1分
…………1分
当n=2时,![]() …………3
…………3
当n=3时,![]() ………5分
………5分
(2) 猜想 ![]() ……………………7分
……………………7分
下面用数学归纳法证明以上猜想。
证明: ①当n= 1 时猜想显然成立。 ……………………8分
② 假设![]() 假设成立,即
假设成立,即![]()
因为 ![]()
又因![]() 得:
得:
![]()
![]()
![]() 从而
从而 ![]()
即n=k+1时,猜想也成立。 ……………………12分
根据 ①② 知,![]() 都成立。 ……………………14分
都成立。 ……………………14分

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 中,
中,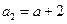 (
(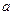 为常数),
为常数), 为
为 项和,且
项和,且 与
与 的等差中项.
的等差中项. ;[来源:学*科*网]
;[来源:学*科*网] 且
且 ,
, 为数列
为数列 的前
的前 的值.
的值. 中,
中, (
( 为常数);
为常数); 是
是 项和,且
项和,且 与
与 的等差中项。K^S*5U.C#O
的等差中项。K^S*5U.C#O ;
; 的表达式,并用数学归纳法加以证明。
的表达式,并用数学归纳法加以证明。 中,
中, =
= (
( 为常数);
为常数); 是
是 项和,且
项和,且 与
与 的等差中项。
的等差中项。 ;
; 的表达式,并用数学归纳法加以证明;
的表达式,并用数学归纳法加以证明; 为坐标的点
为坐标的点 都落在同一直线上。
都落在同一直线上。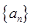 中,
中, (
( 为常数),
为常数), 为
为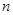 项和,且
项和,且 与
与 的等差中项.
的等差中项. ;[来源:学*科*网]
;[来源:学*科*网]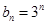 且
且 ,
,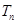 为数列
为数列 的前
的前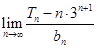 的值.
的值. 中,
中, (
( 为常数);
为常数); 是
是 项和,且
项和,且 与
与 的等差中项。K^S*5U.C#O
的等差中项。K^S*5U.C#O ;
; 的表达式,并用数学归纳法加以证明。
的表达式,并用数学归纳法加以证明。