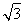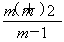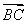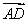题目内容
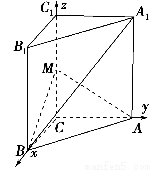
如图,在直三棱柱ABC?A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,A1A=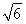 ,M是CC1的中点.
,M是CC1的中点.
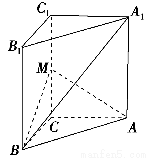
(1)求证:A1B⊥AM;
(2)求二面角B ?AM?C的平面角的大小..
(1)见解析(2)45°
【解析】(1)以点C为原点,CB、CA、CC1所在直线为x,y,z轴,建立空间直角坐标系C-xyz,如图所示,
则B(1,0,0),A(0,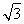 ,0),A1(0,
,0),A1(0,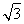 ,
,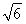 ),M
),M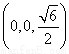 .
.
所以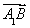 =(1,-
=(1,- ,-
,-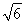 ),
),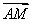 =
= .
.
因为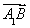 ·
·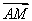 =1×0+(-
=1×0+(-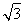 )×(-
)×(-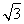 )+(-
)+(-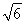 )×
)×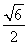 =0,所以A1B⊥AM.
=0,所以A1B⊥AM.
(2)因为ABC ?A1B1C1是直三棱柱,所以CC1⊥平面ABC,又BC?平面ABC,所以CC1⊥BC.
因为∠ACB=90°,即BC⊥AC,又AC∩CC1=C,所以BC⊥平面ACC1A1,即BC⊥平面AMC.
所以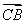 是平面AMC的一个法向量,
是平面AMC的一个法向量,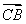 =(1,0,0).
=(1,0,0).
设n=(x,y,z)是平面BAM的一个法向量,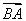 =(-1,
=(-1,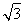 ,0),
,0),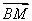 =
= .
.
由 得
得 ,令z=2,得x=
,令z=2,得x=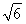 ,y=
,y=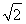 .
.
所以n=(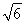 ,
,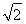 ,2)
,2)
因为|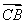 |=1,|n|=2
|=1,|n|=2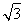 ,所以cos〈
,所以cos〈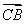 ,n〉=
,n〉=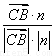 =
=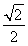 ,
,
因此二面角B ?AM?C的大小为45°

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目