题目内容
已知等差数列 与等比数列
与等比数列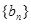 各项都是正数,且
各项都是正数,且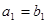 ,
, ,那么一定有( )
,那么一定有( )
A. | B.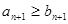 | C. | D. |
B
解析试题分析: 因为 为等差数列,所以
为等差数列,所以 因为
因为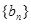 为等比数列,且各项都是正数,所以
为等比数列,且各项都是正数,所以 .又因为
.又因为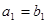 ,
, ,
,
所以
考点:本小题考查等差数列、等比数列的性质及基本不等式的运用.
点评:等差数列和等比数列既相互区别,又相互联系,高考作为考查学生综合能力的选拔性考试,将两类数列综合起来考查是高考的重点.学生容易出现的问题主要有两个方面:一是计算出现失误,二是不能灵活利用等差等比数列的性质,导致运算较为复杂.

练习册系列答案
相关题目
等差数列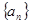 中,
中,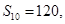 那么
那么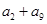 的值是( )
的值是( )
| A.12 | B.24 | C.16 | D.48 |
等差数列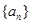 中,
中, ,则
,则 的值是( )
的值是( )
| A.12 | B.24 | C.36 | D.48 |
已知等差数列 的通项公式为
的通项公式为 ,则它的公差为( )
,则它的公差为( )
| A.2 | B.3 | C. | D. |
设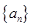 是等差数列,且
是等差数列,且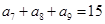 ,则其前15项和
,则其前15项和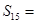 ( )
( )
| A.15 | B.45 | C.75 | D.105 |
设等差数列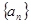 的前
的前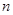 项和为
项和为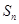 ,若
,若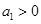 ,
,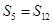 ,则当
,则当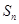 取得最大值时,
取得最大值时,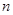 的值为
的值为
| A.7 | B.8 | C.9 | D.8或9 |
已知等差数列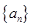 的通项公式
的通项公式 ,则
,则 等于 ( )
等于 ( )
| A.1 | B.2 | C.0 | D.9 |
若实数a,b,c成等比数列,则函数 的图像与
的图像与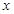 轴交点的个数为( )
轴交点的个数为( )
| A.0个 | B.1个 | C.2个 | D.不能确定 |
已知 ,
, 都是等差数列,前n项和分别记为
都是等差数列,前n项和分别记为 ,若
,若 ,则
,则 ( )
( )
A. | B. | C. | D. |