题目内容
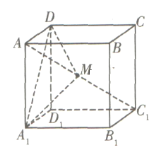
【题目】在棱长为1的正方体![]() 中,点
中,点![]() 是对角线
是对角线![]() 上的动点(点
上的动点(点![]() 与
与![]() 不重合),则下列结论正确的是__________
不重合),则下列结论正确的是__________
①存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
②存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
③![]() 的面积可能等于
的面积可能等于![]() ;
;
④若![]() 分别是
分别是![]() 在平面
在平面![]() 与平面
与平面![]() 的正投影的面积,则存在点
的正投影的面积,则存在点![]() ,使得
,使得![]()
【答案】①②③④
【解析】
根据正方体的结构特征,利用线面位置关系的判定定理和性质定理,以及三角形的面积公式和投影的定义,即可求解,得到答案.
①如图所示,当![]() 是
是![]() 中点时,可知
中点时,可知![]() 也是
也是![]() 中点且
中点且![]() ,
,![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() ,同理可知
,同理可知![]() ,
,
且![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,故正确;
,故正确;

②如图所示,取![]() 靠近
靠近![]() 的一个三等分点记为
的一个三等分点记为![]() ,记
,记![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() ,所以
,所以![]() 为
为![]() 靠近
靠近![]() 的一个三等分点,
的一个三等分点,
则![]() 为
为![]() 中点,又
中点,又![]() 为
为![]() 中点,所以
中点,所以![]() ,且
,且![]() ,
,![]() ,
,![]() ,所以平面
,所以平面![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,故正确;
,故正确;

③如图所示,作![]() ,在
,在![]() 中根据等面积得:
中根据等面积得:![]() ,
,
根据对称性可知:![]() ,又
,又![]() ,所以
,所以![]() 是等腰三角形,
是等腰三角形,
则 ,故正确;
,故正确;

④如图所示,设![]() ,
,![]() 在平面
在平面![]() 内的正投影为
内的正投影为![]() ,
,![]() 在平面
在平面![]() 内的正投影为
内的正投影为![]() ,所以
,所以![]() ,
, ,当
,当![]() 时,解得:
时,解得:![]() ,故正确.
,故正确.

故答案为 ①②③④


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案【题目】交强险是车主须为机动车购买的险种.若普通![]() 座以下私家车投保交强险第一年的费用(基本保费)是
座以下私家车投保交强险第一年的费用(基本保费)是![]() 元,在下一年续保时,实行费率浮动制,其保费与上一年度车辆发生道路交通事故情况相联系,具体浮动情况如下表:
元,在下一年续保时,实行费率浮动制,其保费与上一年度车辆发生道路交通事故情况相联系,具体浮动情况如下表:
类型 | 浮动因素 | 浮动比率 |
| 上一年度未发生有责任的道路交通事故 | 下浮 |
| 上两年度未发生有责任的道路交通事故 | 下浮 |
| 上三年度未发生有责任的道路交通事故 | 下浮 |
| 上一年度发生一次有责任不涉及死亡的道路交通事故 |
|
| 上一年度发生两次及以上有责任不涉及死亡的道路交通事故 | 上浮 |
| 上三年度发生有责任涉及死亡的道路交通事故 | 上浮 |
某一机构为了研究某一品牌![]() 座以下投保情况,随机抽取了
座以下投保情况,随机抽取了![]() 辆车龄满三年的该品牌同型号私家车的下一年续保情况,统计得到如下表格:
辆车龄满三年的该品牌同型号私家车的下一年续保情况,统计得到如下表格:
类型 |
|
|
|
|
|
|
数量 |
|
|
|
|
|
|
以这![]() 辆该品牌汽车的投保类型的频率视为概率.
辆该品牌汽车的投保类型的频率视为概率.
(I)试估计该地使用该品牌汽车的一续保人本年度的保费不超过![]() 元的概率;
元的概率;
(II)记![]() 为某家庭的一辆该品牌车在第四年续保时的费用,求
为某家庭的一辆该品牌车在第四年续保时的费用,求![]() 的分布列和期望.
的分布列和期望.
【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每种单价(![]() 元)试销l天,得到如表单价
元)试销l天,得到如表单价![]() (元)与销量
(元)与销量![]() (册)数据:
(册)数据:
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
(l)根据表中数据,请建立![]() 关于
关于![]() 的回归直线方程:
的回归直线方程:
(2)预计今后的销售中,销量![]() (册)与单价
(册)与单价![]() (元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
(元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
附: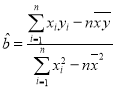 ,
,![]() ,
,![]() ,
,![]() .
.