题目内容
已知函数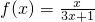 ,数列an满足a1=1,an+1=f(an)(n∈N*).
,数列an满足a1=1,an+1=f(an)(n∈N*).
(1)求数列{an}的通项公式;
(2)记Sn=a1a2+a2a3+…+anan+1,求Sn.
解:(1)由已知得,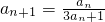 ,整理得
,整理得
∴数列 是首项,公差的等差数列.
是首项,公差的等差数列.
∴ ,
,
故 (6分)
(6分)
(2)∵
Sn=a1a2+a2a3+…+anan+1=
=
= .(13分)
.(13分)
分析:(1)由已知得,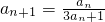 ,从而得到
,从而得到 ,数列
,数列 是首项,公差的等差数列,再利用等差数列的通项公式数列{an}的通项公式即可;
是首项,公差的等差数列,再利用等差数列的通项公式数列{an}的通项公式即可;
(2)根据 利用拆项法即可求出Sn=a1a2+a2a3+…+anan+1.
利用拆项法即可求出Sn=a1a2+a2a3+…+anan+1.
点评:本小题主要考查等差数列的应用、数列的求和、数列与函数的综合等基础知识,考查运算求解能力与转化思想.属于基础题.
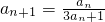 ,整理得
,整理得
∴数列
 是首项,公差的等差数列.
是首项,公差的等差数列.∴
 ,
,故
 (6分)
(6分)(2)∵

Sn=a1a2+a2a3+…+anan+1=

=

=
 .(13分)
.(13分)分析:(1)由已知得,
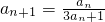 ,从而得到
,从而得到 ,数列
,数列 是首项,公差的等差数列,再利用等差数列的通项公式数列{an}的通项公式即可;
是首项,公差的等差数列,再利用等差数列的通项公式数列{an}的通项公式即可;(2)根据
 利用拆项法即可求出Sn=a1a2+a2a3+…+anan+1.
利用拆项法即可求出Sn=a1a2+a2a3+…+anan+1.点评:本小题主要考查等差数列的应用、数列的求和、数列与函数的综合等基础知识,考查运算求解能力与转化思想.属于基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 若数列{an}满a1=
若数列{an}满a1= ,an+1=f(an),n∈N*,则a2006+a2009+a2010= .
,an+1=f(an),n∈N*,则a2006+a2009+a2010= . 若数列{an}满a1=
若数列{an}满a1= ,an+1=f(an),n∈N*,则a2006+a2009+a2010= .
,an+1=f(an),n∈N*,则a2006+a2009+a2010= .