题目内容
选修4-5:不等式选讲
解不等式|2x-1|<|x|+1.
解:当x<0时,原不等式可化为-2x+1<-x+1,解得x>0.
又∵x<0,∴x不存在,此时,解集为∅.
当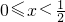 时,原不等式可化为-2x+1<x+1,解得x>0.
时,原不等式可化为-2x+1<x+1,解得x>0.
又∵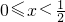 ,∴解集为{x|
,∴解集为{x| }.
}.
当 时,2x-1<x+1,解得
时,2x-1<x+1,解得 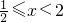 ,故解集为{x|
,故解集为{x|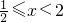 }.
}.
综上,原不等式的解集为 {x| }∪{x|
}∪{x|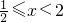 }={x|0<x<2}.
}={x|0<x<2}.
分析:当x<0时,原不等式可化为-2x+1<-x+1,求得解集为∅;当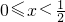 时,原不等式可化为-2x+1<x+1,求得解集为
时,原不等式可化为-2x+1<x+1,求得解集为
{x| }; 当
}; 当 时,2x-1<x+1,求得解集为{x|
时,2x-1<x+1,求得解集为{x|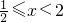 },将这三个解集取并集即得所求.
},将这三个解集取并集即得所求.
点评:本题考查绝对值不等式的解法,体现了分类讨论的数学思想,关键是去掉绝对值,化为与之等价的不等式组来解.
又∵x<0,∴x不存在,此时,解集为∅.
当
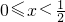 时,原不等式可化为-2x+1<x+1,解得x>0.
时,原不等式可化为-2x+1<x+1,解得x>0.又∵
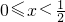 ,∴解集为{x|
,∴解集为{x| }.
}.当
 时,2x-1<x+1,解得
时,2x-1<x+1,解得 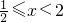 ,故解集为{x|
,故解集为{x|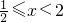 }.
}.综上,原不等式的解集为 {x|
 }∪{x|
}∪{x|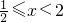 }={x|0<x<2}.
}={x|0<x<2}.分析:当x<0时,原不等式可化为-2x+1<-x+1,求得解集为∅;当
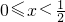 时,原不等式可化为-2x+1<x+1,求得解集为
时,原不等式可化为-2x+1<x+1,求得解集为{x|
 }; 当
}; 当 时,2x-1<x+1,求得解集为{x|
时,2x-1<x+1,求得解集为{x|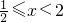 },将这三个解集取并集即得所求.
},将这三个解集取并集即得所求.点评:本题考查绝对值不等式的解法,体现了分类讨论的数学思想,关键是去掉绝对值,化为与之等价的不等式组来解.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目