题目内容

设正整数m，n满足4m+n=30，则m，n恰好使曲线方程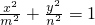 $数学公式$ 表示焦点在x轴上的椭圆的概率是________．

$\text{[math]}$
分析：根据关于m、n的方程4m+n=30，列出所有可能的正整数解有（1，26）、（2，22）、…、（7，2）一共7组，其中使方程 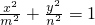$\text{[math]}$ 表示焦点在x轴上椭圆的只有（7，2）这一组，由此结合随机事件的概率公式即可得到本题的概率．
解答：∵正整数m，n满足4m+n=30，
∴基本事件有（1，26）、（2，22）、（3，18）、（4，14）、（5，10）、（6，6）、（7，2），共7组
∵方程 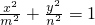$\text{[math]}$ 表示焦点在x轴上的椭圆，
∴m＞n，可得以上7组中只有（7，2）符合题意
因此，曲线方程 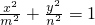$\text{[math]}$ 表示焦点在x轴上的椭圆的概率是 $\text{[math]}$
故答案为： $\text{[math]}$
点评：本题给出曲线方程 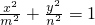$\text{[math]}$ 中的m、n恰好是方程4m+n=30的正整数解，求曲线表示焦点在x轴椭圆的概率，着重考查了椭圆的标准方程、不定方程的整数解讨论和随机事件的概率等知识，属于中档题．

练习册系列答案

宏翔文化中考亮剑系列答案

5年中考江苏13大市中考真题历年回顾精选28套卷系列答案

薪火文化假期百分百系列答案

定位中考三步定位核心大考卷系列答案

中考备战非常领跑金卷系列答案

考易通系列全国中考试题精选系列答案

鸿翔图书中考试题精选系列答案

中考汇编华语中考模拟系列答案

金榜题名新中考全程总复习系列答案

永乾教育寒假作业快乐假期延边人民出版社系列答案

相关题目

各项为正数的数列{a_n} 的前n项和为S_n，且满足：S_n=

（n∈N^*）
（1）求a_n；
（2）设函数f（n）=

)，(n为偶数)

，c_n=f（2ⁿ+4（n∈N^*），求数列{c_n} 的前n项和T_n；
（3）设λ为实数，对满足m+n=3k且m≠n的任意正整数m、n、k，不等式S_m+S_n＞λS_k恒成立，求实数λ的最大值．

已知等差数列{a_n}的前n项和为S_n，且满足S₄=16，S₆=36，
（1）求a_n；
（2）设λ为实数，对任意正整数m，n，不等式S_m+S_n＞λ•S_m+n恒成立，求实数λ的取值范围；
（3）设函数f(n)=

an，n为奇数

c_n=f（2ⁿ⁺²+4）（n∈N^*），求数列{c_n}的前n项和T_n．

集合A₁，A₂，A₃，…，A_n为集合M={1，2，3，…，n}的n个不同的子集，对于任意不大于n的正整数i，j满足下列条件：
①i∉A_i，且每一个A_i至少含有三个元素；
②i∈A_j的充要条件是j∉A_j（其中i≠j）．
为了表示这些子集，作n行n列的数表（即n×n数表），规定第i行第j列数为：a_ij=

．
（1）该表中每一列至少有多少个1；若集合M={1，2，3，4，5，6，7}，请完成下面7×7数表（填符合题意的一种即可）；
（2）用含n的代数式表示n×n数表中1的个数f（n），并证明n≥7；
（3）设数列{a_n}前n项和为f（n），数列{c_n}的通项公式为：c_n=5a_n+1，证明不等式：

＞1对任何正整数m，n都成立．（第1小题用表）

	1	2	3	4	5	6	7
1	0
2		0
3			0
4				0
5					0
6						0
7							0

在等差数列{a_n}中，a₁=1，公差d≠0，a₂²=a₁•a₄，设数列{22-an}的前n项和为S_n．
（1）解不等式：

，求正整数m，n的值；
（2）若数列{b_n}满足b₁=4，b_n+1=b_n²-a_n•b_n+1，求证：

已知各项均为正数的数列{a_n}满足

+anan+1，且a₂+a₄=2a₃+4，其中n∈N^*．
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）设数列{b_n}满足bn=

是否存在正整数m、n（1＜m＜n），使得b₁，b_m，b_n成等比数列？若存在，求出所有的m、n的值，若不存在，请说明理由．