题目内容
4.某房地产公司在2010,对某户型推出两种售房方案:第一种是一次性付款方案,购房的优惠价为28.5万元;第二种是分期付款方式,要求购房时缴纳首付款10万元,然后从第二年起连续十年,在每年的购房日向银行付款2.25万元.假设在此期间银行存款的年利率为3%,若不考虑其他因素,试问:对于购房者来说,采用哪种方案省钱?请计算说明.分析 计算出方案一、二的付款额,即可得出结论.
解答 解:由题意,(28.5-10)×10×3%=5.55,28.5+5.55=34.05
第一年:(28.5-10)×(1+3%)-2.25=16.8
第二年:16.8(1+3%)-2.25=15.1
第三年:15.1(1+3%)-2.25=13.3
第四年:13.3(1+3%)-2.25=11.4
第五年:11.4(1+3%)-2.25=9.5
第六年:9.5(1+3%)-2.25=7.5
第七年:7.5(1+3%)-2.25=5.5
第八年:5.5(1+3%)-2.25=3.4
第九年:3.4(1+3)-2.25=1.3
第十年:1.3(1+3%)-2.25=-0.9 可见第十年时只需要额外出9000元,一共付10+10x22.5+0.9=33.4万元
而第一种方案共34.05万,故分期付款省钱.
点评 本题考查利用数学知识解决实际问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
14.复数z=(-2-i)i在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
12.函数f(x)=sin(2x+$\frac{π}{3}$)-$\frac{1}{2016}$(0≤x≤$\frac{4π}{3}$)的零点为x1,x2,x3(x1<x2<x3),则$\frac{cos({x}_{1}+{x}_{2})}{sin({x}_{2}+{x}_{3})}$=( )
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
10.图中的几何体是下列图中的( )绕线旋转一周得到的.


| A. |  | B. |  | C. |  | D. |  |
7.如图是一个程序框图,则输出的n的值是 ( )
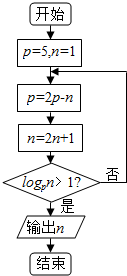

| A. | 29 | B. | 31 | C. | 61 | D. | 63 |