题目内容
设A![]() ,B
,B![]() 是椭圆
是椭圆![]() 上的两点,
上的两点,![]() 为坐标原点,向量
为坐标原点,向量![]() ,向量
,向量![]() 。
。
(1)设![]() ,证明:点M在椭圆上;
,证明:点M在椭圆上;
(2)若点P、Q为椭圆上两点,且![]() ∥
∥![]() 试问:线段PQ能否被直线OA平分?若能平分,请加以证明;若不能平分,请证明理由。
试问:线段PQ能否被直线OA平分?若能平分,请加以证明;若不能平分,请证明理由。
(1)![]()
![]() 又
又![]()
知![]() 把M点坐标代入椭圆方程左边,
把M点坐标代入椭圆方程左边,
得![]()
![]() ∴点M在椭圆上。
∴点M在椭圆上。
(2)1.若![]() ⊥X轴,则OA在X轴上,由
⊥X轴,则OA在X轴上,由![]() ∥
∥![]() ,∴PQ⊥X轴,∵PQ⊥X轴
,∴PQ⊥X轴,∵PQ⊥X轴
∵线段PQ被直线OA平分。
2.若OB∥X轴,同理可证线段PQ被直线OA平分。
2.若![]() 不与X轴垂直或平行,设PQ方程为
不与X轴垂直或平行,设PQ方程为![]()
由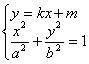
![]()
设![]() 则
则![]()
∴![]() ①
①
![]() ②
②
由①②得PQ中点在直线![]() 上,
上,
又直线OA方程为![]()
![]() PQ中点在直线OA上,故线段PQ被直线OA平分。
PQ中点在直线OA上,故线段PQ被直线OA平分。

练习册系列答案
相关题目
 如图,F1,F2是离心率为
如图,F1,F2是离心率为 (2013•浙江模拟)如图,F1,F2是离心率为
(2013•浙江模拟)如图,F1,F2是离心率为 的椭圆C:
的椭圆C: (a>b>0)的左、右焦点,直线
(a>b>0)的左、右焦点,直线 :x=-
:x=- 将线段F1F2分成两段,其长度之比为1:3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.
将线段F1F2分成两段,其长度之比为1:3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.
 的取值范围.
的取值范围.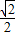 的椭圆C:
的椭圆C: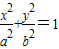 (a>b>0)的左、右焦点,直线l:x=-
(a>b>0)的左、右焦点,直线l:x=- 将线段F1F2分成两段,其长度之比为1:3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.
将线段F1F2分成两段,其长度之比为1:3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.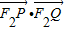 的取值范围.
的取值范围.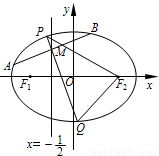
 的椭圆C:
的椭圆C: (a>b>0)的左、右焦点,直线l:x=-
(a>b>0)的左、右焦点,直线l:x=- 将线段F1F2分成两段,其长度之比为1:3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.
将线段F1F2分成两段,其长度之比为1:3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上. 的取值范围.
的取值范围.