题目内容
(13分)如图,在矩形ABCD中,AB=2,BC=![]() ,
,![]() 为等边三角形,又平面PAD⊥平面ABCD.
为等边三角形,又平面PAD⊥平面ABCD.
(Ⅰ)若在边BC上存在一点Q,使PQ⊥QD,求![]() 的取值范围;
的取值范围;
(Ⅱ)当边BC上存在唯一点Q,使PQ⊥QD时,求二面角A-PD-Q的余弦值.
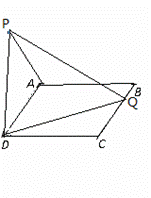
解:(Ⅰ)取AD中点O,连接PO,则PO⊥AD
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,∴PO⊥平面ABCD………2分
建立如图的空间直角坐标系,则![]() ,设Q(t,2,0),
,设Q(t,2,0),
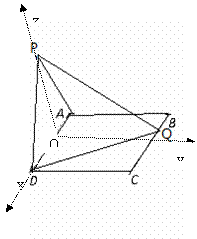 则
则 ![]() =(t,2,-
=(t,2,-![]() ),
),![]() =(t
=(t![]() ,2,0).
,2,0).
∵PQ⊥QD,∴![]() .
.
∴![]() ,等号成立当且仅当t=2.
,等号成立当且仅当t=2.
故![]() 的取值范围为
的取值范围为![]() . …………7分
. …………7分
(Ⅱ)由(Ⅰ)知,当![]() ,
,![]() =8时,边BC上存在唯一点Q,使PQ⊥QD.
=8时,边BC上存在唯一点Q,使PQ⊥QD.
此时Q(2,2,0),D(4,0,0), ![]() .
.
设![]() 是平面
是平面![]() 的法向量,
的法向量,![]() =(2,2,
=(2,2,![]() ),
),
![]() =(-2,2,0).
=(-2,2,0).
由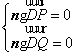 ,得.
,得.
取![]() ,则
,则![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
而![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
设二面角A-PD-Q为![]() ,由
,由![]() .
.
∴二面角A-PD-Q的余弦值为![]() . ……13分
. ……13分

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
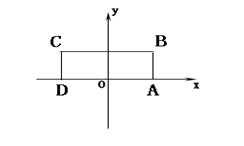 如图,在矩形ABCD中,已知A(2,0)、C(-2,2),点P在BC边上移动,线段OP的垂直平分线交y轴于点E,点M满足
如图,在矩形ABCD中,已知A(2,0)、C(-2,2),点P在BC边上移动,线段OP的垂直平分线交y轴于点E,点M满足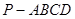 中,底面
中,底面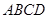 是矩形,知
是矩形,知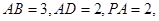
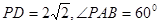 。
。
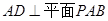 ;
;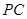 与
与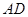 所成的角的余弦值;
所成的角的余弦值;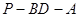 的大小余弦值。
的大小余弦值。 如图,在矩形木板
如图,在矩形木板