题目内容
椭圆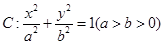 的离心率为
的离心率为 ,两焦点分别为
,两焦点分别为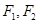 ,点
,点 是椭圆C上一点,
是椭圆C上一点, 的周长为16,设线段MO(O为坐标原点)与圆
的周长为16,设线段MO(O为坐标原点)与圆 交于点N,且线段MN长度的最小值为
交于点N,且线段MN长度的最小值为 .
.
(1)求椭圆C以及圆O的方程;
(2)当点 在椭圆C上运动时,判断直线
在椭圆C上运动时,判断直线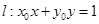 与圆O的位置关系.
与圆O的位置关系.
(1)

(2)直线l与圆O相交
解析试题分析:解:(1)设椭圆C的半焦距为c,则 ,即
,即 ① 1分
① 1分
又 ② 2分
② 2分
联立①②,解得 ,所以
,所以 .
.
所以椭圆C的方程为 . 4分
. 4分
而椭圆C上点 与椭圆中心O的距离为
与椭圆中心O的距离为 ,等号在
,等号在 时成立,…6分
时成立,…6分
而 ,则
,则 的最小值为
的最小值为 ,从而
,从而 ,则圆O的方程为
,则圆O的方程为 . 8分
. 8分
(2)因为点 在椭圆C上运动,所以
在椭圆C上运动,所以 .即
.即 .
.
圆心O到直线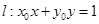 的距离
的距离 . 11分
. 11分
当 ,
, ,
, ,则直线l与圆O相切.
,则直线l与圆O相切.
当 ,
, ,则直线l与圆O相交. 14分
,则直线l与圆O相交. 14分
考点:直线与圆的关系,椭圆的方程
点评:主要是考查了椭圆的性质的运用,以及圆的方程,和直线与圆的位置关系,属于基础题。

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
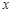 轴上的椭圆C,其长轴长等于4,离心率为
轴上的椭圆C,其长轴长等于4,离心率为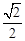 .
.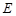 (0,1), 问是否存在直线
(0,1), 问是否存在直线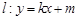 与椭圆
与椭圆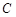 交于
交于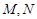 两点,且
两点,且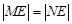 ?若存在,求出
?若存在,求出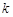 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.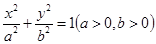 的左焦点F为圆
的左焦点F为圆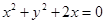 的圆心,且椭圆上的点到点F的距离最小值为
的圆心,且椭圆上的点到点F的距离最小值为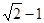 。
。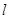 与椭圆交于不同的两点A、B,点M(
与椭圆交于不同的两点A、B,点M(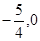 ),证明:
),证明: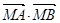 为定值。
为定值。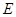 :
: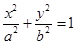 (
(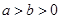 )过点
)过点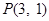 ,其左、右焦点分别为
,其左、右焦点分别为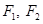 ,且
,且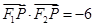 .
.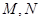 是直线
是直线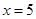 上的两个动点,且
上的两个动点,且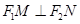 ,则以
,则以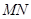 为直径的圆
为直径的圆 是否过定点?请说明理由.
是否过定点?请说明理由.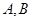 是椭圆
是椭圆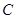 :
: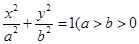 且
且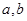 为常数
为常数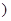 上关于原点对称的两点,点
上关于原点对称的两点,点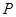 是椭圆上的任意一点,若直线
是椭圆上的任意一点,若直线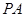 和
和 的斜率都存在,并分别记为
的斜率都存在,并分别记为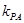 ,
,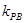 ,那么
,那么 .
.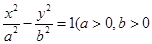 且
且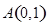 、
、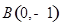 ,
, 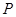 是一个动点, 且直线
是一个动点, 且直线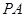 、
、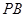 的斜率之积为
的斜率之积为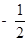 .
.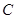 的方程;
的方程; 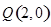 , 过点
, 过点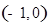 的直线
的直线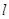 交
交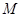 、
、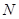 两点, 若对满足条件的任意直线
两点, 若对满足条件的任意直线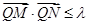 恒成立, 求
恒成立, 求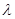 的最小值.
的最小值. 的参数方程为
的参数方程为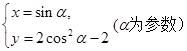 ,曲线
,曲线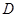 的极坐标方程为
的极坐标方程为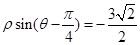 .
.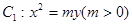 的准线与
的准线与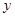 轴交于
轴交于 ,焦点为
,焦点为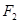 ,若椭圆
,若椭圆 以
以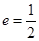 .
. 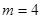 时,求椭圆
时,求椭圆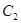 的方程;
的方程; 与直线
与直线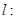
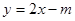 及
及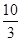 ,求抛物线
,求抛物线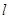 的方程.
的方程. 的长轴长是短轴长的两倍,焦距为
的长轴长是短轴长的两倍,焦距为 .
.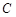 的标准方程;
的标准方程;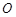 的直线
的直线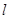 与椭圆
与椭圆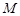 、
、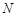 ,且直线
,且直线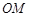 、
、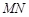 、
、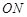 的斜率依次成等比数列,求△
的斜率依次成等比数列,求△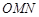 面积的取值范围.
面积的取值范围.