Question

（2011•江西模拟）如图，在底面为等腰梯形的四棱锥P-ABCD中，PA⊥底面ABCD，AB∥CD，AB=7CD=7，BC=AD=5，PA=8，E是PD上任意一点，且

PE

=λ

ED

．
（1）求λ为何值时，PB∥平面ACE；
（2）在（1）的条件下，求三棱锥D-ACE的体积．

Answer 1

分析：（1）连接BD交AC于F，PB∥平面ACE，通过三角形相似，列出比例关系，求出λ的值；
（2）在（1）的条件下，三棱锥D-ACE的体积，转化为V_E-ACD，求出底面面积，E到底面的距离，即可求出体积．

解答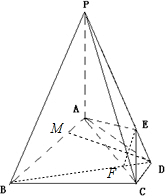：解：（1）连接BD交AC于F，连接EF；
因为PB∥平面ACE．由直线与平面平行的性质可知
PB∥EF，
∴△PDB∽△EDF，
底面ABCD中，AB∥CD，
∴△AFB∽△CFD；
∵AB=7CD=7，
∴λ=

PE

ED

=

BF

FD

=

AB

CD

=7
（2）因为PA⊥底面ABCD，AB=7CD=7，BC=AD=5，PA=8，
λ=

PE

ED

=7，所以E到底面ABCD的距离是1，
过D作DM⊥AB于M，AD=5，AM=3，∴DM=4，
三棱锥D-ACE的体积，就是V_E-ACD，
所以VD-ACE=VE-ACD=

1

3

S△ACD•1= 

1

3

×

1

2

CD•DM×1=  

1

3

•

1

2

•1•4•1=

2

3

点评：本题考查空间几何体的有关证明和计算，三角形的相似，体积的求法，考查计算能力．