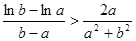题目内容
已知函数![]() 在点
在点![]() 的切线方程为
的切线方程为![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)设![]() ,求证:
,求证:![]() 在
在![]() 上恒成立;
上恒成立;
(Ⅲ)已知![]() ,求证:
,求证:![]() .
.
解:(Ⅰ)将![]() 代入切线方程得
代入切线方程得![]()
∴![]() ,化简得
,化简得![]() …………………………………………2分
…………………………………………2分
![]()
![]()
解得:![]() .
.
∴![]() . …………………………………………4分
. …………………………………………4分
(Ⅱ)由已知得![]() 在
在![]() 上恒成立
上恒成立
化简![]()
即![]() 在
在![]() 上恒成立
上恒成立
设![]() ,
,
![]()
![]() …………………………………………6分
…………………………………………6分
∵![]() ∴
∴![]() ,即
,即![]()
∴![]() 在
在![]() 上单调递增,
上单调递增,![]()
∴![]() 在
在![]() 上恒成立 …………………………………………8分
上恒成立 …………………………………………8分
(Ⅲ)∵![]() ∴
∴![]() ,
,
由(Ⅱ)知![]() 有
有 , …………………………………………10分
, …………………………………………10分
整理得![]()
∴当![]() 时,
时,![]() . …………………………………………12分
. …………………………………………12分

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
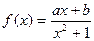 在点
在点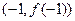 的切线方程为
的切线方程为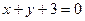
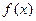 的解析式
的解析式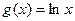 ,求证:
,求证: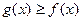 在
在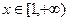 上恒成立
上恒成立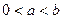 ,求证:
,求证: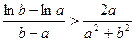
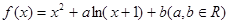 在点
在点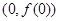 的切线方程为
的切线方程为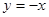
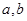 的值;
的值;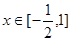 时,
时,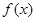 的图像与直线
的图像与直线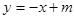 有两个不同的交点,求实数
有两个不同的交点,求实数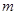 的取值范围;
的取值范围;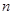 ,不等式
,不等式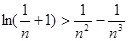 都成立.
都成立.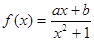 在点
在点 的切线方程为
的切线方程为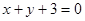
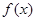 的解析式
的解析式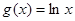 ,求证:
,求证: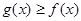 在
在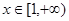 上恒成立
上恒成立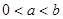 ,求证:
,求证: