题目内容
求证:
(1)
(2)
证明见解析.
解析试题分析:三角恒等式的证明也遵循从繁化简的原则,当然三角函数还有函数名称的转化与角的转化.(1)本题从左向右变化,首先把左边分子用两角差的正弦公式展开,就能证明,当然也可从右向左转化(切化弦), ;(2)这个证明要求我们善于联想,首先左边的和怎么求?能否变为两数的差(利用裂项相消的思想方法)?这个想法实际上在第(1)小题已经为我们做了,只要乘以
;(2)这个证明要求我们善于联想,首先左边的和怎么求?能否变为两数的差(利用裂项相消的思想方法)?这个想法实际上在第(1)小题已经为我们做了,只要乘以 (因为每个分母上的两角的差都是
(因为每个分母上的两角的差都是 ),每个分式都化为两数的差,而且恰好能够前后项相消.
),每个分式都化为两数的差,而且恰好能够前后项相消.
试题解析:证明:(1) 3分
3分 6分
6分
(2)由(1)得 (
( ) 8分
) 8分
可得
 10分
10分 12分
12分
即 . 14分
. 14分
考点:两角差的正弦公式,同角三角函数关系.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 ,且
,且 .
. ;
; .
. ,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.
,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.
 ,求
,求 面积的最大值及此时
面积的最大值及此时 的值.
的值. .
. ,其中
,其中 、
、 为锐角,且
为锐角,且 .
. 的值;
的值;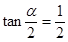 ,求
,求 及
及 的值.
的值. 中,
中, 分别为角
分别为角 的对边,且
的对边,且 .
. .
.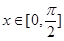 时,求
时,求 的值域;
的值域; 的内角
的内角 的对边分别为
的对边分别为 ,且满足
,且满足 ,
, ,求
,求 的值.
的值.
 ,求b的值.
,求b的值. sin Ccos C-cos2C=
sin Ccos C-cos2C= ,且c=3.
,且c=3. <α<
<α< π,cos(
π,cos( ,sin(
,sin( +β)=
+β)= ,求sin(α+β)的值.
,求sin(α+β)的值.