题目内容

直角坐标系xOy中，
i
，
j
分别是与x，y轴正方向同向的单位向量．在直角三角形ABC中，若
AB
=
i
+k
j
，
AC
=2
i
+
j
，且∠C=90°则k的值是
 
．
分析：利用
BC
=
AC
 -
AB
=
i
+（1-k）
j
，∠C=90°，可得
AC
•
BC
=（ 2
i
+
j
 ）•（
i
+（1-k）
j
 ）=0，解方程求得k的值．
解答：解：∵
BC
=
AC
 -
AB
=2
i
+
j
-
i
-k
j
=
i
+（1-k）
j
，∠C=90°，
∴
AC
•
BC
=（ 2
i
+
j
 ）•（
i
+（1-k）
j
 ）=2+0+0 （1-k）=0，
∴k=3，
故答案为3．
点评：本题考查两个向量的数量积公式的应用，两个向量坐标形式的运算，两个向量垂直的性质，得到 
AC
•
BC
=
2+0+0 （1-k）=0，是解题的关键．
练习册系列答案
相关题目
在平面直角坐标系xOy中，已知以O为圆心的圆与直线l：y=mx+（3-4m），（m∈R）恒有公共点，且要求使圆O的面积最小．
（1）写出圆O的方程；
（2）圆O与x轴相交于A、B两点，圆内动点P使|
PA
|、|
PO
|、|
PB
|成等比数列，求
PA
•
PB
的范围；
（3）已知定点Q（-4，3），直线l与圆O交于M、N两点，试判断
QM
•
QN
×tan∠MQN是否有最大值，若存在求出最大值，并求出此时直线l的方程，若不存在，给出理由．
在平面直角坐标系xOy中，已知点A（0，2）、B（1，1），直线l 经过点B且与线段OA相交．则直线 l 倾斜角α的取值范围是
（　　）
在平面直角坐标系xOy中，P为直线y=-x-2上一点，Q为函数f（x）=
2x
（x＞0）的图象上一点，则线段PQ长的最小值是
 
．
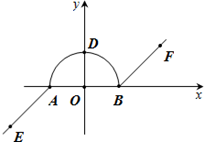精英家教网如图，在平面直角坐标系xOy中，我把由两条射线AE，BF和以AB为直径的半圆所组成的图形叫作图形C（注：不含AB线段）．已知A（-1，0），B（1，0），AE∥BF，且半圆与y轴的交点D在射线AE的反向延长线上．
（1）求两条射线AE，BF所在直线的距离；
（2）当一次函数y=x+b的图象与图形C恰好只有一个公共点时，写出b的取值范围；当一次函数y=x+b的图象与图形C恰好只有两个公共点时，写出b的取值范围．
在平面直角坐标系xOy中，不等式组
1≤x+y≤3
-1≤x-y≤1
表示图形的面积等于（　　）
A、1B、2C、3D、4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网