Question

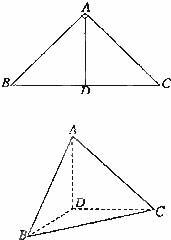
如图，在△ABC中，∠ABC=45°，∠BAC=90°，AD高，沿AD把是BC上的△ABD折起，使∠BDC=90°．

（Ⅰ）证明：平面ADB⊥平面BDC；

（Ⅱ）设BD=1，求三棱锥D﹣ABC的表面积．

Answer 1

解答：

解：（Ⅰ）∵折起前AD是BC边上的高，

∴当△ABD折起后，AD⊥DC，AD⊥DB，

又DB∩DC=D，

∴AD⊥平面BDC，

∵AD⊂平面ABD．

∴平面ADB⊥平面BDC

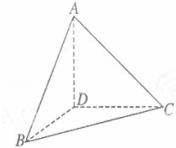
（Ⅱ）由（Ⅰ）知，DA⊥DB，DB⊥DC，DC⊥DA，

∵DB=DA=DC=1，∴AB=BC=CA=，

从而

所以三棱锥D﹣ABC的表面积为：

点评：

解决平面图形翻折问题的关键是看准翻折后没有发生变化的位置关系，抓住翻折后仍然垂直的直线作为条件，从而解决问题．