��Ŀ����
��֪������ x2=4y�Ľ�������Բ C��
+
=1(a��b��0)һ�����㣬��ԲC��������Ϊ
������һԲOԲ��������ԭ�㣬�뾶Ϊ
��I������ԲC��ԲO�ķ��̣�
������֪����P��0��
����ֱ��l����ԲC�ڵ�һ������ֻ��һ�������㣬��ֱ��l��ԲO�صõ��ҳ���
������֪M��x0��y0����ԲO������һ�㣬��M����ֱ��l1��l2��ʹ��l1��l2����ԲC��ֻ��һ�������㣬��֤��l1��l2��
| x2 |
| n2 |
| y2 |
| b2 |
| ||
| 2 |
| a2+b2 |
��I������ԲC��ԲO�ķ��̣�
������֪����P��0��
| a2+b2 |
������֪M��x0��y0����ԲO������һ�㣬��M����ֱ��l1��l2��ʹ��l1��l2����ԲC��ֻ��һ�������㣬��֤��l1��l2��
��I����x2=4y�ɵ������߽�������Ϊ��0��1������b=1��
�֡�e=
����
=
����a2=b2+c2����a2=4��
��
=
��
����ԲC�ķ���Ϊ
+y2=1��ԲO�ķ���Ϊx2+y2=5��
���߹���P��0��
����ֱ��l����ԲC�ڵ�һ������ֻ��һ�������㣬
��ֱ��l��б�ʴ��ڣ���l�ķ���Ϊy=kx+
��k��0
��
����x2+4(kx+
)2=4��
����1+4k2��x2+8
kx+16=0��
����=(8
k)2-64(1+4k2)=0��
��k2=1����k��0��k=-1��
��ֱ��l����Ϊy=-x+
��
Բ��O��ֱ��l����Ϊy=-x+
��
Բ��O��ֱ��l�ľ���d=
=
��
��ֱ��l��ԲO�صõ��ҳ�Ϊ2
=
��
����֤��������M������Ϊ��2��1������2��-1������-2��-1������-2��1����
������ĵ�ֱ�������������ֱ��l1��l2��
��һ��ֱ��б��Ϊ0������һ��б�ʲ����ڣ���l1��l2
��ֱ��l1��l2б�ʶ����ڣ������M����Բֻ��һ���������ֱ�߷���Ϊy-y0=k��x-x0����
��
����x2+4[kx+��y0-kx0��]2=4��
����1+4k2��x2+8k��y0-kx0��•x+4��y0-kx0��2-4=0��
���=[8k��y0-kx0��]2-4��1+4k2��[4��y0-kx0��2-4]=0��
����ã�4-x02��k2+2x0y0k+1-y02=0��
��x02+y02=5��
�ࣨ4-x02��k2+2x0yk+x02-4=0��
��l1��l2��б�ʷֱ�Ϊk1��k2����Ϊl1��l2����Բ��ֻ��һ�������㣬
����k1��k2���㣨4-x02��k2+2x0yk+x02-4=0��
��k1•k2=
=-1��
��l1��l2��
�֡�e=
| ||
| 2 |
| c2 |
| a2 |
| 3 |
| 4 |
��
| a2+b2 |
| 5 |
����ԲC�ķ���Ϊ
| x2 |
| 4 |
���߹���P��0��
| 5 |
��ֱ��l��б�ʴ��ڣ���l�ķ���Ϊy=kx+
| 5 |
��
|
| 5 |
����1+4k2��x2+8
| 5 |
����=(8
| 5 |
��k2=1����k��0��k=-1��
��ֱ��l����Ϊy=-x+
| 5 |
Բ��O��ֱ��l����Ϊy=-x+
| 5 |
Բ��O��ֱ��l�ľ���d=
| ||
|
| ||
| 2 |
��ֱ��l��ԲO�صõ��ҳ�Ϊ2
5-(
|
| 10 |
����֤��������M������Ϊ��2��1������2��-1������-2��-1������-2��1����
������ĵ�ֱ�������������ֱ��l1��l2��
��һ��ֱ��б��Ϊ0������һ��б�ʲ����ڣ���l1��l2
��ֱ��l1��l2б�ʶ����ڣ������M����Բֻ��һ���������ֱ�߷���Ϊy-y0=k��x-x0����
��
|
����1+4k2��x2+8k��y0-kx0��•x+4��y0-kx0��2-4=0��
���=[8k��y0-kx0��]2-4��1+4k2��[4��y0-kx0��2-4]=0��
����ã�4-x02��k2+2x0y0k+1-y02=0��
��x02+y02=5��
�ࣨ4-x02��k2+2x0yk+x02-4=0��
��l1��l2��б�ʷֱ�Ϊk1��k2����Ϊl1��l2����Բ��ֻ��һ�������㣬
����k1��k2���㣨4-x02��k2+2x0yk+x02-4=0��
��k1•k2=
| x02-4 |
| 4-x02 |
��l1��l2��

��ϰ��ϵ�д�
�����Ŀ
��֪������x2+my=0�ϵĵ㵽���㣨0��4���͵���ֱ��y=-4�ľ�����ȣ���m=��������
A��
| ||
B��-
| ||
| C��16 | ||
| D��-16 |
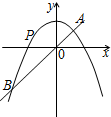 ��ͼ����֪������y=4-x2��ֱ��y=3x����������ֱ�ΪA��B����P���������ϴ�A��B�˶�����P��ͬ�ڵ�A��B����
��ͼ����֪������y=4-x2��ֱ��y=3x����������ֱ�ΪA��B����P���������ϴ�A��B�˶�����P��ͬ�ڵ�A��B����