Question

已知函数f（x）=xsinx，对于[-

π

2

，

π

2

]上的任意x₁，x₂，有如下条件：
①

x

2 1

＞

x

2 2

；②x₁＞x₂；③x₁＞x₂，且

x1+x2

2

＞0．其中能使f（x₁）＞f（x₂）恒成立的条件序号是

①③

．（写出所有满足条件的序号）

Answer 1

分析：先判断函数的奇偶性，易知是偶函数，同时再判断单调性，根据函数性质作出草图，即可得到结论．

解答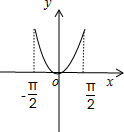：解：由已知得f（x）是偶函数，且在区间[-

π

2

，0]上递减，在[0，

π

2

]上递增，
作出函数的草图，如图所示：
由图象可知，f（x₁）＞f（x₂）?|x₁|＞|x₂|，即x₁²＞x₂²．故①符合，②不符合；
由x₁＞x₂，且

x1+x2

2

＞0，知x₁＞0，
若x₂＞0，则显然f（x₁）＞f（x₂）成立；
若x₂＜0，由x₁+x₂＞0，得x₁＞-x₂，
即|x₁|＞|x₂|，有f（x₁）＞f（x₂）成立，故③符合；
故答案为：①③．

点评：本题主要考查函数单调性的定义和奇偶性在对称区间上单调性．