Question

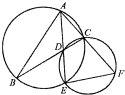如图，在△ABC中，∠BAC的平分线分别交BC、和△ABC的外接圆于点D和E，延长AC交过C，D，E三点的圆于点F．
（1）求证：EF²=ED•EA；
（2）若AE=6．EF=3，求AF•AC的值．

Answer 1

分析：（1）利用同弧或等弧所对的圆周角相等及三角形相似即可得出；
（2）由割线定理即可得出．

解答：解：（1）如图所示，连接DF、EC，
由同弧或等弧所对的圆周角相等可得：∠DFE=∠DCE，∠DCE=∠BAE=∠EAC，
∴∠DFE=∠EAF，又∠DEF公用，
∴△DEF∽△FEA，∴

EF

EA

=

ED

EF

，∴EF²=ED•EA．
（2）由（1）可知：ED=

EF2

EA

=

32

6

=

3

2

，
由割线定理得AD•AE=AC•AF，
∴AC•AF=（AE-DE）•AE=(6-

3

2

)×6=27．

点评：熟练掌握同弧或等弧所对的圆周角相等、三角形相似的性质定理及割线定理是解题的关键．