题目内容
求椭圆 的长轴长、短轴长、离心率、焦点和顶点坐标,并用描点法画出这个椭圆.
的长轴长、短轴长、离心率、焦点和顶点坐标,并用描点法画出这个椭圆.
 的长轴长、短轴长、离心率、焦点和顶点坐标,并用描点法画出这个椭圆.
的长轴长、短轴长、离心率、焦点和顶点坐标,并用描点法画出这个椭圆.解:根据椭圆的标准方程,得
a=5,b =3,c=
因此,长轴长2a=10,短轴长2b=6.
∴离心率
焦点为F1(-4,0)和F2(4,O),
顶点为A1(-5,0),A2(5,0),B1(0,-3),B2(0,3).
将方程变形为 (-5≤x≤5),
(-5≤x≤5),
根据y= (-5≤x≤5)可求出椭圆的两个顶点及其在第一象限内一些点的坐标(x,y),列表如下:
(-5≤x≤5)可求出椭圆的两个顶点及其在第一象限内一些点的坐标(x,y),列表如下:

先描点画出第一象限的图形,再利用椭圆的对称性画出整个椭圆(如图).


a=5,b =3,c=

因此,长轴长2a=10,短轴长2b=6.
∴离心率

焦点为F1(-4,0)和F2(4,O),
顶点为A1(-5,0),A2(5,0),B1(0,-3),B2(0,3).
将方程变形为
 (-5≤x≤5),
(-5≤x≤5),根据y=
 (-5≤x≤5)可求出椭圆的两个顶点及其在第一象限内一些点的坐标(x,y),列表如下:
(-5≤x≤5)可求出椭圆的两个顶点及其在第一象限内一些点的坐标(x,y),列表如下: 
先描点画出第一象限的图形,再利用椭圆的对称性画出整个椭圆(如图).


练习册系列答案
相关题目
 的长轴长是短轴长的两倍,焦距为
的长轴长是短轴长的两倍,焦距为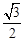 .
. 的标准方程;
的标准方程;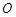 的直线
的直线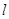 与椭圆
与椭圆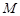 、
、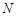 ,且直线
,且直线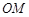 、
、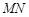 、
、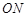 的斜率依次成等比数列,求△
的斜率依次成等比数列,求△ 面积的取值范围.
面积的取值范围.