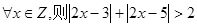题目内容
下列四个命题,其中为真命题的是
①方程2x2+4x+y=0表示的曲线一定经过坐标原点,
②不等式x2+4x+5≤0的解集为空集,
③方程xy=0表示的曲线关于直线y=x对称,
④若sinα=sinβ,则α=β.
①②③
①②③
;(写出所有的真命题序号)①方程2x2+4x+y=0表示的曲线一定经过坐标原点,
②不等式x2+4x+5≤0的解集为空集,
③方程xy=0表示的曲线关于直线y=x对称,
④若sinα=sinβ,则α=β.
分析:根据曲线方程的概念,点在曲线上的充要条件是点的坐标是曲线方程的解,∴只需验证点的坐标是不是方程的解,就可判定点在不在曲线上,利用一元二次函数图象与一元二次方程的根,可分析求解一元二次不等式的解集;点(a、b)关于y=x对称点是(b、a),用方程验证即可.
解答:解:∵原点(0,0)的坐标是方程2x2+4x+y=0的解,∴曲线一定过坐标原点,①√;
∵△=42-4×5=16-20=-4<0,函数y=x2+4x+5 的图象全部在x轴上方,∴x2+4x+5≤0的解集为∅,∴②√;
∵对曲线上的任一点P(a,b)关于y=x的对称点Q(b,a),满足方程ba=0,∴Q(b,a)在曲线上,∴曲线 xy=0,关于y=x 直线对称,③√;
∵sin
=sin
=
,而
≠
,∴④×;
故答案是①②③
∵△=42-4×5=16-20=-4<0,函数y=x2+4x+5 的图象全部在x轴上方,∴x2+4x+5≤0的解集为∅,∴②√;
∵对曲线上的任一点P(a,b)关于y=x的对称点Q(b,a),满足方程ba=0,∴Q(b,a)在曲线上,∴曲线 xy=0,关于y=x 直线对称,③√;
∵sin
| π |
| 6 |
| 5π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
故答案是①②③
点评:本题借助真假命题的判断,考查了一元二次不等式的解集;曲线方程的概念及曲线对称的判定方法等知识.

练习册系列答案
相关题目
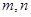 是两条不同的直线,
是两条不同的直线, 是两个不重合的平面,给定下列四个命题,其中为真命题的是( )
是两个不重合的平面,给定下列四个命题,其中为真命题的是( ) ②
②
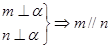 ④
④
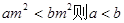 ”的逆命题.
”的逆命题.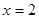 是
是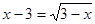 的充分不必要条件.
的充分不必要条件.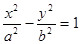 和椭圆
和椭圆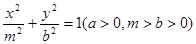 的离心率之积大于1,则以
的离心率之积大于1,则以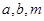 为边长的三角形是钝角三角形.
为边长的三角形是钝角三角形.