题目内容
 如图,在边长为4的正方形ABCD的边上有一动点P,沿折线BCDA由点B(起点)向点A(终点)移动,设点P移动的路程为x,△APB的面积为y.
如图,在边长为4的正方形ABCD的边上有一动点P,沿折线BCDA由点B(起点)向点A(终点)移动,设点P移动的路程为x,△APB的面积为y.(1)求y关于x的函数关系式y=f(x);
(2)画出y=f(x)的图象;
(3)若△APB的面积不小于2,求x的取值范围.
分析:(1)先求出定义域,然后根据点P的位置进行分类讨论,根据三角形的面积公式求出每一段△ABP的面积与P移动的路程间的函数关系式,最后用分段函数进行表示即可;
(2)根据每一段的函数解析式画出每一段的函数图象,即可得到y=f(x)的图象;
(3)利用△APB的面积不小于2,结合函数解析式,建立不等式,即可求x的取值范围.
(2)根据每一段的函数解析式画出每一段的函数图象,即可得到y=f(x)的图象;
(3)利用△APB的面积不小于2,结合函数解析式,建立不等式,即可求x的取值范围.
解答: 解:(1)由于x=0与x=12时,三点A、B、P不能构成三角形,故这个函数的定义域为(0,12).
解:(1)由于x=0与x=12时,三点A、B、P不能构成三角形,故这个函数的定义域为(0,12).
当0<x≤4时,S=f(x)=
•4•x=2x;
当4<x≤8时,S=f(x)=8;
当8<x<12时,S=f(x)=
•4•(12-x)=2(12-x)=24-2x.
∴这个函数的解析式为f(x)=
(2)其图形为右上图;
(3)当0<x≤4时,2x≥2,∴1≤x≤4;当4<x≤8时,S=8,满足题意;
当8<x<12时,S=24-2x≥2,∴8<x≤11
综上,1≤x≤11.
 解:(1)由于x=0与x=12时,三点A、B、P不能构成三角形,故这个函数的定义域为(0,12).
解:(1)由于x=0与x=12时,三点A、B、P不能构成三角形,故这个函数的定义域为(0,12).当0<x≤4时,S=f(x)=
| 1 |
| 2 |
当4<x≤8时,S=f(x)=8;
当8<x<12时,S=f(x)=
| 1 |
| 2 |
∴这个函数的解析式为f(x)=
|
(2)其图形为右上图;
(3)当0<x≤4时,2x≥2,∴1≤x≤4;当4<x≤8时,S=8,满足题意;
当8<x<12时,S=24-2x≥2,∴8<x≤11
综上,1≤x≤11.
点评:本题主要考查了函数解析式的求解,以及分段函数的图象,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
相关题目
 如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.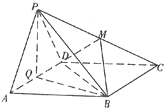 如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M、Q分别为PC,AD的中点.
如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M、Q分别为PC,AD的中点. (2013•资阳模拟)如图,在边长为2的正六边形ABCDEF中,P是△CDE内(含边界)的动点,设向量
(2013•资阳模拟)如图,在边长为2的正六边形ABCDEF中,P是△CDE内(含边界)的动点,设向量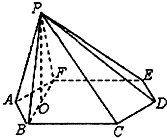 (2012•武清区一模)如图,六棱锥P-ABCDEF的底面ABCDEF是边长为l的正六边形,顶点P在底面上的射影是BF的中点O.
(2012•武清区一模)如图,六棱锥P-ABCDEF的底面ABCDEF是边长为l的正六边形,顶点P在底面上的射影是BF的中点O.