题目内容
5.函数f(x)=xcosx的导数为cosx-xsinx.分析 利用导数的运算法则(μv)′=μ′v+μv′及导数的公式cosx′=-sinx,求出导函数即可.
解答 解:根据(μv)′=μ′v+μv′可得
y′=x′cosx+x(cosx)′=cosx-xsinx.
故答案为:cosx-xsinx.
点评 求函数的导数值时,先根据函数的形式选择合适的导数运算法则及导数公式,属于基础题.

练习册系列答案
相关题目
13.用分析法证明问题时是从要证明的结论出发,逐步寻求使它成立的( )
| A. | 充要条件 | B. | 充分条件 | ||
| C. | 必要条件 | D. | 既不充分也不必要条件 |
20.已知数列{an}满足对任意n∈N*,都有anan+1an+2an+3=24,且a1=1,a2=2,a3=3,则a1+a2+a3+…+a2015=( )
| A. | 5030 | B. | 5031 | C. | 5033 | D. | 5036 |
17.长时间用手机上网严重影响着学生身心健康及学习成绩,某校为了解高二年级A,B两班学生手机上网的时长,分别从这两个班中随机抽取6名同学进行调查,将他们平均每周手机上网时长作为样本数据,A班(单位:小时/每周):9,37,11,20,13,24;B班:11,36,21,25,27,12(单位:小时/每周).注:规定学生平均每周手机上网的时长超过21小时,称为“过度用网”.
(Ⅰ)根据两组数据绘制茎叶图(图中的茎表示十位数字,叶表示个位数字),根据样本数据,分别估计A,B两班的学生平均每周上网时长的平均值,并比较哪个班的学生平均上网时间较长;
(II)从A班、B班的样本中各随机抽取2名学生的数据,记“过度用网”的学生人数为ξ,写出ξ的分布列和数学期望E(ξ).
(Ⅰ)根据两组数据绘制茎叶图(图中的茎表示十位数字,叶表示个位数字),根据样本数据,分别估计A,B两班的学生平均每周上网时长的平均值,并比较哪个班的学生平均上网时间较长;
| A班 | B班 | |
| 0 | ||
| 1 | ||
| 2 | ||
| 3 |
14.函数y=sin(x+$\frac{π}{6}$)的一个递减区间是( )
| A. | [-$\frac{π}{2}$,$\frac{π}{2}$] | B. | [-π,0] | C. | [-$\frac{2π}{3}$,$\frac{2π}{3}$] | D. | [$\frac{π}{3}$,$\frac{4π}{3}$] |
15.直线x-y+3=0的倾斜角所在的区间是( )
| A. | (0,$\frac{π}{4}$) | B. | [$\frac{π}{4}$,$\frac{π}{2}$) | C. | ($\frac{π}{2}$,$\frac{3π}{4}$) | D. | [$\frac{3π}{4}$,π) |
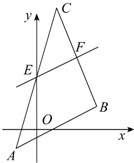 已知△ABC的三顶点是A(-1,-1),B(3,1),C(1,6).直线l平行于AB,交AC,BC分别于E,F,且E、F分别是AC、BC的中点.求:
已知△ABC的三顶点是A(-1,-1),B(3,1),C(1,6).直线l平行于AB,交AC,BC分别于E,F,且E、F分别是AC、BC的中点.求: