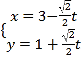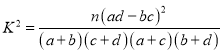题目内容
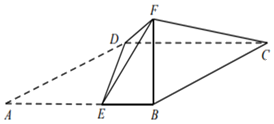
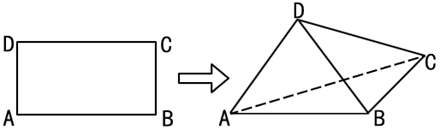
【题目】如图,四边形![]() 是矩形,沿对角线
是矩形,沿对角线![]() 将
将![]() 折起,使得点
折起,使得点![]() 在平面
在平面![]() 上的射影恰好落在边
上的射影恰好落在边![]() 上.
上.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
【答案】(I)见解析;(II)![]() .
.
【解析】试题分析:(1)先证明![]() . 结合
. 结合![]() ,得
,得![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)以点![]() 为原点,线段
为原点,线段![]() 所在的直线为
所在的直线为![]() 轴,线段
轴,线段![]() 所在的直线为
所在的直线为![]() 轴,建立空间直角坐标系,用向量法求解即可.
轴,建立空间直角坐标系,用向量法求解即可.
试题解析:(1)设点![]() 在平面
在平面![]() 上的射影为点
上的射影为点![]() ,连接
,连接![]()
则![]() 平面
平面![]() ,所以
,所以![]() .
.
因为四边形![]() 是矩形,所以
是矩形,所以![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
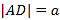
(2)方法1:在矩形![]() 中,过点
中,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,连结
,连结![]() .
.
因为![]() 平面
平面![]()
![]() ,又DM∩DE=D
,又DM∩DE=D
所以![]() 平面
平面![]()
![]() ,
,
所以![]() 为二面角
为二面角![]() 的平面角.
的平面角.
设![]() ,则
,则![]() .
.
在![]() 中,易求出
中,易求出![]() ,
, ![]() .
.
在![]() 中,
中, ![]() ,
,
所以![]() .
.
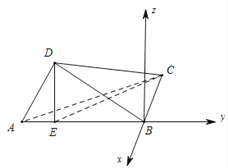
方法2:以点![]() 为原点,线段
为原点,线段![]() 所在的直线为
所在的直线为![]() 轴,线段
轴,线段![]() 所在的直线为
所在的直线为![]() 轴,建立空间直角坐标系,如图所示.
轴,建立空间直角坐标系,如图所示.
设![]() ,则
,则![]() ,所以
,所以![]() ,
, ![]() .
.
由(I)知![]() ,又
,又![]() ,所以
,所以![]() °,
°,![]() °,那么
°,那么![]() ,
, ![]() ,
, ![]() ,
,
所以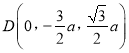 ,所以
,所以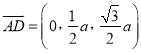 ,
, ![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则![]() 即
即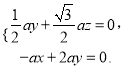
取![]() ,则
,则![]() ,
, ![]() ,所以
,所以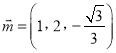 .
.
因为平面![]() 的一个法向量为
的一个法向量为![]() ,
,
所以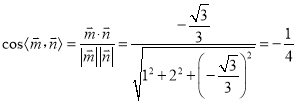 .
.
所以求二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】金秋九月,丹桂飘香,某高校迎来了一大批优秀的学生.新生接待其实也是和社会沟通的一个平台.校团委、学生会从在校学生中随机抽取了160名学生,对是否愿意投入到新生接待工作进行了问卷调查,统计数据如下:
愿意 | 不愿意 | |
男生 | 60 | 20 |
女士 | 40 | 40 |
(1)根据上表说明,能否有99%把握认为愿意参加新生接待工作与性别有关;
(2)现从参与问卷调查且愿意参加新生接待工作的学生中,采用按性别分层抽样的方法,选取10人.若从这10人中随机选取3人到火车站迎接新生,设选取的3人中女生人数为![]() ,写出
,写出![]() 的分布列,并求
的分布列,并求![]() .
.
附: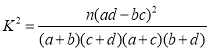 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |