题目内容
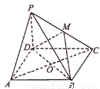
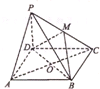 如图,四棱锥P-A BCD中,底面ABCD为菱形,BD⊥面PAC,A C=10,PA=6,cos∠PCA=
如图,四棱锥P-A BCD中,底面ABCD为菱形,BD⊥面PAC,A C=10,PA=6,cos∠PCA=| 4 | 5 |
(Ⅰ)证明PC⊥平面BMD;
(Ⅱ)若三棱锥M-BCD的体积为14,求菱形ABCD的边长.
分析:(I)先根据线面垂直的性质证明PC⊥BD,再在△PAC中利用余弦定理求出PC的长,从而证出PA∥MO,进一步得PC⊥MO,最后根据线面垂直的判定定理可得PC⊥平面BMD;
(II)由题意知,将三棱锥M-BCD的体积转换成三棱锥C-BMD的体积,再利用棱锥的体积公式列出等式求出菱形ABCD的对角线的长,从而得出菱形ABCD的边长.
(II)由题意知,将三棱锥M-BCD的体积转换成三棱锥C-BMD的体积,再利用棱锥的体积公式列出等式求出菱形ABCD的对角线的长,从而得出菱形ABCD的边长.
解答:解:(I)∵BD⊥面PAC,PC?面PAC,
∴PC⊥BD,
△PAC中,AC=10,PA=6,cos∠PCA=
,
∴PA2=PC2+AC2-2PC•ACcos∠PCA,
∴PC=8,
连结MO,∵M是PC的中点,O是AC的中点,
∴PA∥MO,∴PC⊥MO,又∵BD∩MO=O,
∴PC⊥平面BMD;
(II)由题意知:三棱锥M-BCD的体积为14,
即VM-BCD=VC-MBD=
S△MBD×CM=
BD•MO•CM=14,
∵CM=
PC=4,MO=
PA=3,
∴BD=7,
∴菱形ABCD的边长AB=
=
.
∴PC⊥BD,
△PAC中,AC=10,PA=6,cos∠PCA=
| 4 |
| 5 |
∴PA2=PC2+AC2-2PC•ACcos∠PCA,
∴PC=8,
连结MO,∵M是PC的中点,O是AC的中点,
∴PA∥MO,∴PC⊥MO,又∵BD∩MO=O,
∴PC⊥平面BMD;
(II)由题意知:三棱锥M-BCD的体积为14,
即VM-BCD=VC-MBD=
| 1 |
| 3 |
| 1 |
| 6 |
∵CM=
| 1 |
| 2 |
| 1 |
| 2 |
∴BD=7,
∴菱形ABCD的边长AB=
| AO2+OB2 |
| ||
| 2 |
点评:本题考查证明线面垂直的方法,直线与平面垂直的判定、性质的应用,棱锥的体积等,考查空间想象能力,属于中档题.

练习册系列答案
相关题目
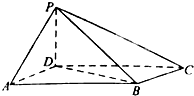 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD. 如图,四棱锥P-ABCD中,PA⊥底面ABCD,PC⊥AD.底面ABCD为梯形,AB∥DC,AB⊥BC.PA=AB=BC,点E在棱PB上,且PE=2EB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,PC⊥AD.底面ABCD为梯形,AB∥DC,AB⊥BC.PA=AB=BC,点E在棱PB上,且PE=2EB.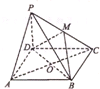 如图,四棱锥P-A BCD中,底面ABCD为菱形,BD⊥面PAC,A C=10,PA=6,cos∠PCA=
如图,四棱锥P-A BCD中,底面ABCD为菱形,BD⊥面PAC,A C=10,PA=6,cos∠PCA= ,M是PC的中点.
,M是PC的中点. ,M是PC的中点.
,M是PC的中点.