题目内容
若不等式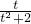 ≤a≤
≤a≤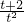 ,在t∈(0,2]上恒成立,则a的取值范围是________.
,在t∈(0,2]上恒成立,则a的取值范围是________.

分析:欲使不等式
 在t∈(0,2]上恒成立,只需求函数
在t∈(0,2]上恒成立,只需求函数 在t∈(0,2]上的最大值,
在t∈(0,2]上的最大值,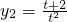 在t∈(0,2]上的最小值,而函数
在t∈(0,2]上的最小值,而函数 在t∈(0,2]上的最大值,利用基本不等式进行求解,
在t∈(0,2]上的最大值,利用基本不等式进行求解,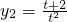 在t∈(0,2]上的最小值,利用配方法和二次函数的性质进行求解.
在t∈(0,2]上的最小值,利用配方法和二次函数的性质进行求解.解答:要使不等式
 在t∈(0,2]上恒成立,只需求函数
在t∈(0,2]上恒成立,只需求函数 在t∈(0,2]上的最大值,
在t∈(0,2]上的最大值,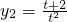 在t∈(0,2]上的最小值.
在t∈(0,2]上的最小值.而
 ,根据基本不等式最值成立的条件可知函数在t=
,根据基本不等式最值成立的条件可知函数在t= 时取得最大值为
时取得最大值为
 ,从而函数在t=2时取得最小值为1
,从而函数在t=2时取得最小值为1所以实数a的取值范围是

故答案为:

点评:本题主要考查了不等式,函数的最值问题与恒成立结合的综合类问题,在解答的过程当中充分体现了恒成立的思想、二次函数求最值的方法和问题转化的能力,属于中档题.

练习册系列答案
相关题目
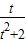 ≤a≤
≤a≤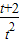 ,在t∈(0,2]上恒成立,则a的取值范围是 .
,在t∈(0,2]上恒成立,则a的取值范围是 .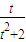 ≤a≤
≤a≤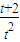 ,在t∈(0,2]上恒成立,则a的取值范围是 .
,在t∈(0,2]上恒成立,则a的取值范围是 .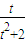 ≤a≤
≤a≤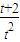 ,在t∈(0,2]上恒成立,则a的取值范围是 .
,在t∈(0,2]上恒成立,则a的取值范围是 .