题目内容
已知椭圆 (a>b>0)的左右顶点为A1,A2,上下顶点为B1,B2,左右焦点为F1,F2,若△F1B1F2为等腰直角三角形
(a>b>0)的左右顶点为A1,A2,上下顶点为B1,B2,左右焦点为F1,F2,若△F1B1F2为等腰直角三角形
(1)求椭圆的离心率;
(2)若△A1B1A2的面积为6 ,求椭圆的方程.
,求椭圆的方程.
解:(1)∵△F1B1F2为等腰直角三角形,∴b=c
∴a2-c2=c2
∴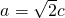
∴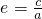 =
= ;
;
(2)∵△A1B1A2的面积为6 ,
,
∴
∴ab=6 ,
,
∵
∴b= ,a=2
,a=2
∴椭圆的方程为 .
.
分析:(1)利用△F1B1F2为等腰直角三角形,可得b=c,由此可求椭圆的离心率;
(2)根据△A1B1A2的面积为6 ,结合
,结合 ,可求椭圆的方程.
,可求椭圆的方程.
点评:本题考查椭圆的方程,考查椭圆的几何性质,考查学生的计算能力,属于中档题.
∴a2-c2=c2
∴
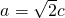
∴
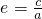 =
= ;
;(2)∵△A1B1A2的面积为6
 ,
,∴

∴ab=6
 ,
,∵

∴b=
 ,a=2
,a=2
∴椭圆的方程为
 .
.分析:(1)利用△F1B1F2为等腰直角三角形,可得b=c,由此可求椭圆的离心率;
(2)根据△A1B1A2的面积为6
 ,结合
,结合 ,可求椭圆的方程.
,可求椭圆的方程.点评:本题考查椭圆的方程,考查椭圆的几何性质,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
 =2
=2 ,
, ·
· =
= ,求椭圆的方程.
,求椭圆的方程. (a>b>0),点
(a>b>0),点 在椭圆上。
在椭圆上。 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆 有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B. 分)
分) (a>b>0)的离心率
(a>b>0)的离心率 ,焦距是函数
,焦距是函数 的零点.
的零点. 与椭圆交于
与椭圆交于 、
、 两点,
两点, ,求k的值.
,求k的值.