题目内容
如图,ABCD—A′B′C′D′为长方体,底面是边长为a的正方形,高为2a,M,N分别是CD和AD的中点.(1)判断四边形MNA′C′的形状;
(2)求四边形MNA′C′的面积.
解:(1)连结AC.因为M,N分别是CD,AD的中点,所以MN![]()
![]() AC.
AC.
因为ABCD—A′B′C′D′是长方体,所以AC![]() C′A′为矩形.所以A′C′
C′A′为矩形.所以A′C′![]()
![]() AC.所以MN
AC.所以MN![]()
![]() A′C′.所以四边形MNA′C′是梯形.
A′C′.所以四边形MNA′C′是梯形.
在△A′AN和△C′CM中,
因为∠A′AN=∠C′CM=90°,
AA′=CC′=2a,AN=CM=![]() a,
a,
所以△A′AN≌△C′CM.所以A′N=C′M.
所以四边形MNA′C′是等腰梯形.
(2)由A′C′=![]() a,MN=
a,MN=![]() a,
a,
A′N=C′M=![]() a,
a,
得梯形的高h=![]() a,
a,
所以,S梯形MNAC=![]() (
(![]() a+
a+![]() a)×
a)×![]() a=
a=![]() a.
a.

练习册系列答案
相关题目
如图ABCD-A1B1C1D1是正方体,B1E1=D1F1=
,则BE1与DF1所成的角的余弦值是( )

| A1B1 |
| 4 |

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 12、如图,A,B,C,D四点都在平面a,b外,它们在a内的射影A1,B1,C1,D1是平行四边形的四个顶点,在b内的射影A2,B2,C2,D2在一条直线上,求证:ABCD是平行四边形.
12、如图,A,B,C,D四点都在平面a,b外,它们在a内的射影A1,B1,C1,D1是平行四边形的四个顶点,在b内的射影A2,B2,C2,D2在一条直线上,求证:ABCD是平行四边形.
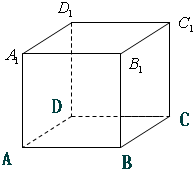 如图ABCD-A1B1C1D1为正方体,一只青蛙开始在顶点A处,它每次可随意跳到相邻三顶点之一,若在五次内跳到C1点,则停止跳动;若5次内不能跳到C1点,跳完五次也停止跳动,求:
如图ABCD-A1B1C1D1为正方体,一只青蛙开始在顶点A处,它每次可随意跳到相邻三顶点之一,若在五次内跳到C1点,则停止跳动;若5次内不能跳到C1点,跳完五次也停止跳动,求: