题目内容
【题目】已知函数![]() ,其中
,其中![]() 为常数,
为常数,![]() 为自然对数的底数.
为自然对数的底数.
(1)当![]() 时,求
时,求![]() 的最大值;
的最大值;
(2)若![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() 的最大值为
的最大值为![]() .(2)
.(2)![]() 的值为
的值为![]() .
.
【解析】
试题分析:(1)![]() 时,
时,![]() ,定义域为
,定义域为![]() .求导得
.求导得![]() ,列表讨论当
,列表讨论当![]() 变化时,
变化时,![]() ,
,![]() 变化情况,可得
变化情况,可得![]() 的最大值;(2)求导得
的最大值;(2)求导得![]() ,分
,分![]() 和
和![]() 两种情况讨论,当
两种情况讨论,当![]() 时
时![]()
![]() 不符合题意;当
不符合题意;当![]() 时,分
时,分![]() 和
和![]() 讨论可得到
讨论可得到![]() 的值
的值
试题解析:(1)当![]() 时,
时,![]() ,定义域为
,定义域为![]() .
.
求导得![]() ,
,
令![]() ,得
,得![]() ,
,
当![]() 变化时,
变化时,![]() ,
,![]() 变化情况如下:
变化情况如下:
|
| 1 |
|
|
|
|
|
|
|
|
|
由表可知![]() 的最大值为
的最大值为![]() .
.
(2)求导得![]() .
.
①当![]() 时,
时,![]() 恒成立,此时
恒成立,此时![]() 在
在![]() 上单调递增,最大值为
上单调递增,最大值为![]() ,解得
,解得![]() ,不符合要求;
,不符合要求;
②当![]() 时,令
时,令![]() ,得
,得![]() ,
,
若![]() ,此时
,此时![]() 在
在![]() 上恒成立,此时
上恒成立,此时![]() 在
在![]() w上单调递增,最大值为
w上单调递增,最大值为![]() ,解得
,解得![]() ,不符合要求;
,不符合要求;
若![]() ,此时
,此时![]() 在
在![]() 上成立,
上成立,![]() 在
在![]() 上成立,此时
上成立,此时![]() 在
在![]() 上先增后减,最大值为
上先增后减,最大值为![]() ,解得
,解得![]() ,符合要求.
,符合要求.
综上可知,![]() 的值为
的值为![]() .
.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
【题目】“奶茶妹妹”对某时间段的奶茶销售量及其价格进行调查,统计出售价![]() 元和销售量
元和销售量![]() 杯之间的一组数据如下表所示:
杯之间的一组数据如下表所示:
价格 | 5 | 5.5 | 6.5 | 7 |
销售量 | 12 | 10 | 6 | 4 |
通过分析,发现销售量![]() 对奶茶的价格
对奶茶的价格![]() 具有线性相关关系.
具有线性相关关系.
(Ⅰ)求销售量![]() 对奶茶的价格
对奶茶的价格![]() 的回归直线方程;
的回归直线方程;
(Ⅱ)欲使销售量为![]() 杯,则价格应定为多少?
杯,则价格应定为多少?
附:线性回归方程为![]() ,其中
,其中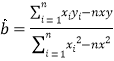 ,
,![]()