题目内容
12.已知集合A={x|3≤x≤6,B={y|y=2x,2≤x<3}.(1)分别求A∩B;(CRB)∪A
(2)已知C={x|a≤x≤a+1},若C⊆B,求实数a的取值范围.
分析 (1)先求出B,由此利用交集、补集、并集的概念能求出A∩B、(∁RB)∪A.
(2)由C={x|a≤x≤a+1},C⊆B,利用子集的概念能求出实数a的取值范围是[4,7].
解答 解:(1)∵集合A={x|3≤x≤6,B={y|y=2x,2≤x<3}={y|4≤y<8},
∴A∩B={x|4≤x≤6},
∁RB={x|x<4或x>8},(∁RB)∪A=(-∞,6)∪[8,+∞).
(2)∵C={x|a≤x≤a+1},C⊆B,
∴$\left\{\begin{array}{l}{a≥4}\\{a+1≤8}\end{array}\right.$,解得4≤a≤7,
∴实数a的取值范围是[4,7].
点评 本题考查交集、补集、并集、实数的取值范围的求法,是基础题,解题时要注意交集、补集、并集、子集等基本概念的合理运用.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
20.已知集合A={-1,1,2,},B={x|(x-1)(x-3)≤0},则A∩B=( )
| A. | .{1,2} | B. | {1} | C. | {-1,1} | D. | .∅ |
17. 如图,棱长都相等的平行六面体ABCD-A′B′C′D′中,∠DAB=∠A′AD=∠A′AB=60°,则二面角A′-BD-A的余弦值为( )
如图,棱长都相等的平行六面体ABCD-A′B′C′D′中,∠DAB=∠A′AD=∠A′AB=60°,则二面角A′-BD-A的余弦值为( )
 如图,棱长都相等的平行六面体ABCD-A′B′C′D′中,∠DAB=∠A′AD=∠A′AB=60°,则二面角A′-BD-A的余弦值为( )
如图,棱长都相等的平行六面体ABCD-A′B′C′D′中,∠DAB=∠A′AD=∠A′AB=60°,则二面角A′-BD-A的余弦值为( )| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
4.设点M(0,-5),N(0,5),△MNP的周长为36,则△MNP的顶点P的轨迹方程为( )
| A. | $\frac{{y}^{2}}{169}$+$\frac{{x}^{2}}{25}$=1(x≠0) | B. | $\frac{{y}^{2}}{169}$+$\frac{{x}^{2}}{144}$=1(x≠0) | ||
| C. | $\frac{{x}^{2}}{169}$+$\frac{{y}^{2}}{25}$=1(y≠0) | D. | $\frac{{y}^{2}}{169}$+$\frac{{x}^{2}}{25}$=1(y≠0) |
1.已知函数f(x)=|log2|x-2||+k有四个零点x1,x2,x3,x4,则x1+x2+x3+x4+k的取值范围为( )
| A. | (8,+∞) | B. | (4,+∞) | C. | (-∞,8) | D. | (-∞,4) |
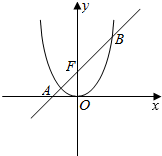 如图,已知抛物线C:x2=2py(0<p<4),其上一点M(4,y0)到其焦点F的距离为5,过焦点F的直线l与抛物线C交于A,B左、右两点.
如图,已知抛物线C:x2=2py(0<p<4),其上一点M(4,y0)到其焦点F的距离为5,过焦点F的直线l与抛物线C交于A,B左、右两点.