题目内容
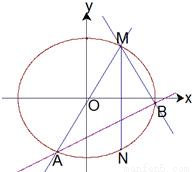
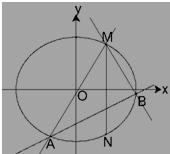
已知两点M(2,3),N(2,-3)在椭圆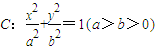 上,斜率为
上,斜率为 的直线l与椭圆C交于点A,B(A,B在直线MN两侧),且四边形MANB面积的最大值为
的直线l与椭圆C交于点A,B(A,B在直线MN两侧),且四边形MANB面积的最大值为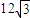 .求椭圆C的方程.
.求椭圆C的方程.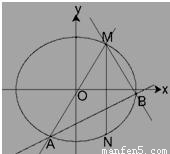
【答案】分析:先设直线l的方程为 (m∈R)并代入代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得a,b值,即得椭圆C的方程,从而解决问题.
(m∈R)并代入代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得a,b值,即得椭圆C的方程,从而解决问题.
解答:解:设直线l的方程为 (m∈R)并代入b2x2+a2y2=a2b2
(m∈R)并代入b2x2+a2y2=a2b2
得: x2+ma2x+a2m2-a2b2=0
x2+ma2x+a2m2-a2b2=0
设A(x1,y1),B(x2,y2)(x1,2,y1,2∈R)
则 ,
,
又
=
显然当m=0时,SMANB= =
= (1)
(1)
由题意|MN|=6(2)4b2+9a2=a2b2(3)
联立(1)、(2)、(3)解得:a2=16,b2=12
即椭圆C的方程为: .
.
点评:本题主要考查椭圆的基本性质和直线与椭圆的位置关系.本题考查用待定系数法求椭圆的标准方程,利用方程的思想解决具体问题,体现了方程的数学思想.
 (m∈R)并代入代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得a,b值,即得椭圆C的方程,从而解决问题.
(m∈R)并代入代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得a,b值,即得椭圆C的方程,从而解决问题.解答:解:设直线l的方程为
 (m∈R)并代入b2x2+a2y2=a2b2
(m∈R)并代入b2x2+a2y2=a2b2得:
 x2+ma2x+a2m2-a2b2=0
x2+ma2x+a2m2-a2b2=0设A(x1,y1),B(x2,y2)(x1,2,y1,2∈R)
则
 ,
,
又

=

显然当m=0时,SMANB=
 =
= (1)
(1)由题意|MN|=6(2)4b2+9a2=a2b2(3)
联立(1)、(2)、(3)解得:a2=16,b2=12
即椭圆C的方程为:
 .
.点评:本题主要考查椭圆的基本性质和直线与椭圆的位置关系.本题考查用待定系数法求椭圆的标准方程,利用方程的思想解决具体问题,体现了方程的数学思想.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 已知两点M(2,3),N(2,-3)在椭圆
已知两点M(2,3),N(2,-3)在椭圆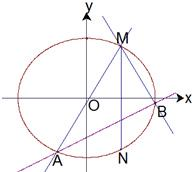 (2010•台州二模)已知两点M(2,3),N(2,-3)在椭圆
(2010•台州二模)已知两点M(2,3),N(2,-3)在椭圆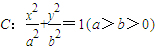 上,斜率为
上,斜率为 的直线l与椭圆C交于点A,B(A,B在直线MN两侧),且四边形MANB面积的最大值为
的直线l与椭圆C交于点A,B(A,B在直线MN两侧),且四边形MANB面积的最大值为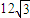 .w
.w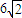 ,试判断△MAB的形状.
,试判断△MAB的形状.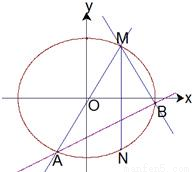
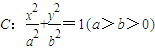 上,斜率为
上,斜率为 的直线l与椭圆C交于点A,B(A,B在直线MN两侧),且四边形MANB面积的最大值为
的直线l与椭圆C交于点A,B(A,B在直线MN两侧),且四边形MANB面积的最大值为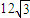 .w
.w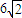 ,试判断△MAB的形状.
,试判断△MAB的形状.