题目内容
(2011•南通模拟)已知函数f(x)=5sinxcosx-5
cos2x(其中x∈R).
求:
①函数f(x)的最小正周期;
②函数f(x)的单调递减区间;
③函数f(x)图象的对称轴.
| 3 |
求:
①函数f(x)的最小正周期;
②函数f(x)的单调递减区间;
③函数f(x)图象的对称轴.
分析:利用三角函数的恒等变换化简函数的解析式为 f(x)=5sin(2x-
)-
,由此求得f(x)最小正周期、单调区间、对称轴.
| π |
| 3 |
5
| ||
| 2 |
解答:解∵f(x)=
sin2x-5
=
sin2x-
cos2x-
=5(
sin2x-
cos2x)-
=5sin(2x-
)-
,
∴①f(x)最小正周期T=π;
②由2kπ+
≤2x-
≤2kπ+
,k∈Z,得kπ+
≤x≤kπ+
,k∈Z,
故f(x)的单调减区间为[kπ+
, kπ+
],k∈z.
③由2x-
=kπ+
(k∈Z),求得f(x)的对称轴为x=
+
(k∈Z).
| 5 |
| 2 |
| 3 |
| 1+cos2x |
| 2 |
| 5 |
| 2 |
5
| ||
| 2 |
5
| ||
| 2 |
=5(
| 1 |
| 2 |
| ||
| 2 |
5
| ||
| 2 |
| π |
| 3 |
5
| ||
| 2 |
∴①f(x)最小正周期T=π;
②由2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| 5π |
| 12 |
| 11π |
| 12 |
故f(x)的单调减区间为[kπ+
| 5π |
| 12 |
| 11π |
| 12 |
③由2x-
| π |
| 3 |
| π |
| 2 |
| kπ |
| 2 |
| 5π |
| 12 |
点评:本题主要考查三角函数的恒等变换,符合三角函数的周期性、单调性和对称性,属于中档题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 (2011•南通模拟)
(2011•南通模拟)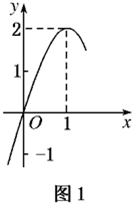 如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.
如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.