Question

不等式|5x-x²|＜6的解集为（    ）

A.{x|x＜2或x＞3}                  B.{x|-1＜x＜2或3＜x＜6}

C.{x|-1＜x＜6}                     D.{x|2＜x＜3}

Answer 1

思路解析：可以利用|x|＜a的结论进行转化，然后解一元二次不等式，取交集可得结果，本题还可以用数形法求结果.

方法一：由|5x-x²|＜6,得|x²-5x|＜6.

∴-6＜x²-5x＜6.

∴

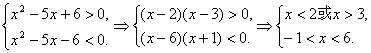
∴-1＜x＜2或3＜x＜6.

∴原不等式的解集为{x|-1＜x＜2或3＜x＜6}

方法二：作函数y=x²-5x的图象.

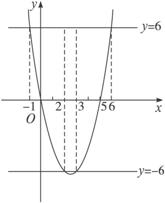
    |x²-5x|＜6表示函数图象中直线y=-6和直线y=6之间相应部分的自变量的集合.解方程

x²-5x=6,得x₁=-1,x₂=6.

x²-5x=-6,得x₁′=2,x₂′=3.

即得到不等式的解集是{x|-1＜x＜2或3＜x＜6}.

答案：B