Question

如果一个正方形的四个点都在三角形的三边上，则该正方形是该三角形的内接正方形，那么面积为4的锐角△ABC的内接正方形面积的最大值为

2

．

Answer 1

分析：先求正方形的边长，而图中有三角形相似，利用相似三角形的对应高之比等于相似比而求出正方形的边长，最后利用基本不等式求出正方形面积的最大值．

解答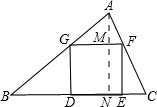：解：如图，作AN⊥BC于N交GF与M，
∵四边形GDEF是正方形
∴GF=GD=MN，GF∥BC
∴△AGF∽△ABC
∴

AM

AN

=

GF

BC

．
设正方形的边长为x．
∴

h-x

h

=

x

a

解得x=

ah

a+h

．
由于三角形的面积为4，∴ah=8，
∴x=

ah

a+h

=

8

a+h

≤

8

2 ah

=

2

，当且仅当a=h时取等号，
∴△ABC的内接正方形面积的最大值为

2

2=2．
故答案为：2．

点评：本题考查了相似三角形的判定与性质以及基本不等式，重点是相似三角形的对应高之比等于相似比的运用．