题目内容
已知f(x)=a-x(a>0且a≠1),且f(-2)>f(-3),则a的取值范围是
- A.a>0
- B.a>1
- C.a<1
- D.0<a<1
D
分析:由f(-2)>f(-3)知,函数f(x)=a-x =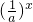 是增函数,故有
是增函数,故有  >1,从而得到a的取值范围.
>1,从而得到a的取值范围.
解答:∵f(-2)>f(-3),
∴f(x)=a-x =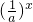 是增函数,
是增函数,
∴ >1,
>1,
∴0<a<1,
则a的取值范围是 0<a<1,
故选 D.
点评:本题考查指数函数的单调性,当m>1时,y=mx是个增函数.
分析:由f(-2)>f(-3)知,函数f(x)=a-x =
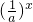 是增函数,故有
是增函数,故有  >1,从而得到a的取值范围.
>1,从而得到a的取值范围.解答:∵f(-2)>f(-3),
∴f(x)=a-x =
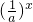 是增函数,
是增函数,∴
 >1,
>1,∴0<a<1,
则a的取值范围是 0<a<1,
故选 D.
点评:本题考查指数函数的单调性,当m>1时,y=mx是个增函数.

练习册系列答案
相关题目
 ,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间
,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间 上的值域为
上的值域为 ,若存在,求出a的值;若不存在,请说明理由.
,若存在,求出a的值;若不存在,请说明理由. ,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间
,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间 上的值域为
上的值域为 ,若存在,求出a的值;若不存在,请说明理由.
,若存在,求出a的值;若不存在,请说明理由. x3,x∈(-2,2)为正常数.
x3,x∈(-2,2)为正常数.
 (当且仅当a=b时取等号)”推广到三个正数时结论是正确的,试写出推广后的结论(无需证明);
(当且仅当a=b时取等号)”推广到三个正数时结论是正确的,试写出推广后的结论(无需证明); x3,x∈(-2,2)为正常数.
x3,x∈(-2,2)为正常数.
 (当且仅当a=b时取等号)”推广到三个正数时结论是正确的,试写出推广后的结论(无需证明);
(当且仅当a=b时取等号)”推广到三个正数时结论是正确的,试写出推广后的结论(无需证明);