题目内容
对于a∈R,直线(x+y-1)-a(x+1)=0恒过定点P,则以P为圆心,
为半径的圆的方程是( )
| 5 |
| A.x2+y2+2x+4y=0 | B.x2+y2+2x-4y=0 |
| C.x2+y2-2x+4y=0 | D.x2+y2-2x-4y=0 |
联解
,可得x=-1,y=2
∴直线(x+y-1)-a(x+1)=0恒过定点P(-1,2)
因此以P为圆心,
为半径的圆的方程是(x+1)2+(y-2)2=5
化成一般式可得x2+y2+2x-4y=0
故选:B
|
∴直线(x+y-1)-a(x+1)=0恒过定点P(-1,2)
因此以P为圆心,
| 5 |
化成一般式可得x2+y2+2x-4y=0
故选:B

练习册系列答案
相关题目
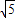 为半径的圆的方程是( )
为半径的圆的方程是( )