题目内容
关于函数 (x∈R),有下列命题:
(x∈R),有下列命题:①y=f(x)可改写为
 ;
;②y=f(x)是2π为最小正周期的周期函数;
③y=f(x)图象关于点(
 ,0)对称;
,0)对称;④y=f(x)图象关于点直线
 对称.
对称.其中正确命题的序号是( )
A.①③④
B.③④
C.①④
D.①③
【答案】分析:由函数 (x∈R),利用正弦型曲线的周期性、对称性和三角函数的诱导公式能求出结果.
(x∈R),利用正弦型曲线的周期性、对称性和三角函数的诱导公式能求出结果.
解答:解:∵ (x∈R),
(x∈R),
∴y=f(x)=3cos[ -(2x+
-(2x+ )]
)]
=3cos( -2x)=3cos(2x-
-2x)=3cos(2x- ),
),
故①正确;
∵ (x∈R),
(x∈R),
∴f(x)的最小正周期T= =π,故②不正确;
=π,故②不正确;
∵ (x∈R)的对称中心是(
(x∈R)的对称中心是( ,0),k∈Z
,0),k∈Z
∴当k=0时,y=f(x)图象关于点( ,0)对称,故③正确;
,0)对称,故③正确;
∵ (x∈R)的对称轴是x=
(x∈R)的对称轴是x= ,k∈Z
,k∈Z
故④不正确.
故选D.
点评:本题考查命题的真假判断,解题时要认真审题,注意三角函数的性质的合理运用.
 (x∈R),利用正弦型曲线的周期性、对称性和三角函数的诱导公式能求出结果.
(x∈R),利用正弦型曲线的周期性、对称性和三角函数的诱导公式能求出结果.解答:解:∵
 (x∈R),
(x∈R),∴y=f(x)=3cos[
 -(2x+
-(2x+ )]
)]=3cos(
 -2x)=3cos(2x-
-2x)=3cos(2x- ),
),故①正确;
∵
 (x∈R),
(x∈R),∴f(x)的最小正周期T=
 =π,故②不正确;
=π,故②不正确;∵
 (x∈R)的对称中心是(
(x∈R)的对称中心是( ,0),k∈Z
,0),k∈Z∴当k=0时,y=f(x)图象关于点(
 ,0)对称,故③正确;
,0)对称,故③正确;∵
 (x∈R)的对称轴是x=
(x∈R)的对称轴是x= ,k∈Z
,k∈Z故④不正确.
故选D.
点评:本题考查命题的真假判断,解题时要认真审题,注意三角函数的性质的合理运用.

练习册系列答案
相关题目
 (x∈R),有下列命题:
(x∈R),有下列命题:
 对称.
对称. 对称.
对称. (x∈R)有下列命题:
(x∈R)有下列命题: 个单位得到;
个单位得到; 对称;
对称;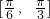 上是减函数.
上是减函数. (x∈R)有下列命题:
(x∈R)有下列命题: 个单位得到;
个单位得到; 对称;
对称; 上是减函数.
上是减函数. (x∈R)有下列命题:
(x∈R)有下列命题: 个单位得到;
个单位得到; 对称;
对称; 上是减函数.
上是减函数.