题目内容

函数f（x）=tanωx（ω＞0）的图象的相邻两支截直线y=
π
4
所得线段长为2，则f(-
4
3
)的值是（　　）
分析：根据题意得函数的周期T=
π
4
，结合正切函数周期公式算出w=2，得到函数表达式再将-
4
3
代入并结合正切的诱导公式加以计算，即可得到答案．
解答：解：∵函数图象的相邻两支截直线y=
π
4
所得线段长为2，
∴函数的周期T=2，
可得
π
w
=2，可得w=
π
2

函数表达式为f（x）=tan
π
2
x，
可得f(-
4
3
)=tan（-
2π
3
）=tan
π
3
=
3

故选：C
点评：本题给出函数y=tanwx（w＞0）满足的条件，求特殊的函数值．着重考查了正切函数的周期公式、诱导公式等知识，属于基础题．
练习册系列答案
相关题目
有以下四个命题：
①函数f（x）=sin（
π
3
-2x）的一个增区间是[
5π
12
，
11π
12
]；
②若函数f（x）=sin（ωx+φ）为奇函数，则φ为π的整数倍；
③对于函数f（x）=tan（2x+
π
3
），若f（x1）=f（x2），则x1-x2必是π的整数倍；
④函数y=2sin（2x+
π
3
）的图象关于点（
π
3
，0）对称．
其中正确的命题是
 
．（填上正确命题的序号）
设函数f（x）=tan（ωx+?），（ω＞0），条件P：“f（0）=0”；条件Q：“f（x）为奇函数”，则P是Q的（　　）
（2012•南京二模）下列四个命题
①“?x∈R，x2-x+1≤1”的否定；
②“若x2+x-6≥0，则x＞2”的否命题；
③在△ABC中，“A＞30°“sinA＞
12
”的充分不必要条件；
④“函数f（x）=tan（x+φ）为奇函数”的充要条件是“φ=kπ（k∈z）”．
其中真命题的序号是
②
②
．（把真命题的序号都填上）
已知函数f（x）=tan（2x+
π
4
）
（I）求该函数的定义域，周期及单调区间；
（II）若f（θ）=
1
7
，求
2cos2
θ
2
-sinθ-1
2
sin(θ+
π
4
)
的值．
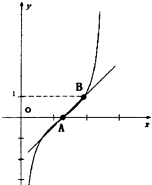精英家教网如图为函数f（x）=tan（
π
4
x-
π
2
）的部分图象，点A为函数f（x）在y轴右侧的第一个零点，点B在函数f（x）图象上，它的纵坐标为1，直线AB的倾斜角等于
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网