题目内容
已知0＜θ＜π，且sinθ+cosθ=
，求tanθ．
| 7 | 13 |
分析：由sinθ+cosθ=
，利用平方关系可得sinθcosθ=-
．由于0＜θ＜π，可得sinθ＞0＞cosθ．于是sinθ-cosθ=
=
．因此
=
，利用“弦化切”tanθ=
，即可得出．
| 7 |
| 13 |
| 60 |
| 169 |
| (sinθ-cosθ)2 |
| 17 |
| 13 |
| sinθ+cosθ |
| sinθ-cosθ |
| 7 |
| 17 |
| sinθ |
| cosθ |
解答：解：∵sinθ+cosθ=
，
∴(sinθ+cosθ)2=
，∴sin2θ+cos2θ+2sinθcosθ=
，∴sinθcosθ=-
．
∵0＜θ＜π，∴sinθ＞0＞cosθ．
∴sinθ-cosθ=
=
=
=
．
∴
=
，
∵tanθ=
，
∴
=
，
解得tanθ=-
．
| 7 |
| 13 |
∴(sinθ+cosθ)2=
| 49 |
| 169 |
| 49 |
| 169 |
| 60 |
| 169 |
∵0＜θ＜π，∴sinθ＞0＞cosθ．
∴sinθ-cosθ=
| (sinθ-cosθ)2 |
| sin2θ+cos2θ-2sinθcosθ |
1+
|
| 17 |
| 13 |
∴
| sinθ+cosθ |
| sinθ-cosθ |
| 7 |
| 17 |
∵tanθ=
| sinθ |
| cosθ |
∴
| tanθ+1 |
| tanθ-1 |
| 7 |
| 17 |
解得tanθ=-
| 12 |
| 5 |
点评：本题考查了三角函数的基本关系式、“弦化切”方法、正弦余弦函数的单调性，属于中档题．
练习册系列答案
相关题目
的周期为
，且当
时，函数
的最小值为0．
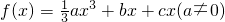，已知a＜b＜c，且
，曲线y=f（x）在x=1处取极值．