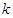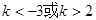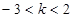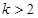题目内容
下面给出四个命题的表述:
①直线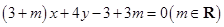 恒过定点
恒过定点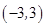 ;
;
②线段AB的端点B的坐标是(3,4),A在圆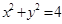 上运动,则线段AB的中点M的轨迹方程
上运动,则线段AB的中点M的轨迹方程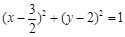 ;
;
③已知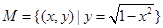 ,
,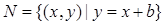 ,若
,若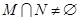 ,
,
则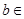
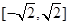 ;
;
④已知圆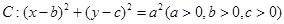 与
与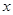 轴相交,与
轴相交,与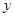 轴相离,则直线
轴相离,则直线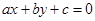 与直线
与直线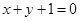 的交点在第二象限.其中表述正确的是( )
的交点在第二象限.其中表述正确的是( )
①直线
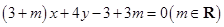 恒过定点
恒过定点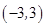 ;
;②线段AB的端点B的坐标是(3,4),A在圆
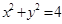 上运动,则线段AB的中点M的轨迹方程
上运动,则线段AB的中点M的轨迹方程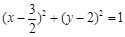 ;
;③已知
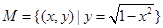 ,
,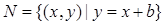 ,若
,若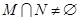 ,
,则
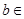
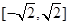 ;
;④已知圆
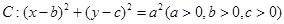 与
与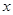 轴相交,与
轴相交,与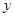 轴相离,则直线
轴相离,则直线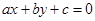 与直线
与直线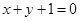 的交点在第二象限.其中表述正确的是( )
的交点在第二象限.其中表述正确的是( )| A.①②④ | B.①②③ | C.①③ | D.①②③④ |
A
解:因为命题1中,直线方程能变形为m(x+3)+4y+3x-3=0=0,表示的过两直线的交点的直线系,因此必定过点(-3,3)
命题2中,利用代入点的方法,设所求的点的坐标,利用中点公式,表示已知点与未知点的关系,代入已知的方程中得到结论。
命题3中,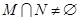 ,则直线与半圆有公共点,需要
,则直线与半圆有公共点,需要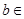
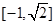 ,因此错误
,因此错误
命题4中,利用设y=0,x=0,得到方程分别无解和有解,来判定两直线交点的位置即可。
命题2中,利用代入点的方法,设所求的点的坐标,利用中点公式,表示已知点与未知点的关系,代入已知的方程中得到结论。
命题3中,
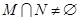 ,则直线与半圆有公共点,需要
,则直线与半圆有公共点,需要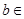
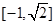 ,因此错误
,因此错误命题4中,利用设y=0,x=0,得到方程分别无解和有解,来判定两直线交点的位置即可。

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
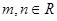 ,若直线
,若直线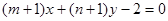 与圆
与圆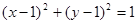 相切,则m + n的取值范围是
相切,则m + n的取值范围是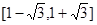
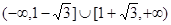
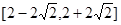
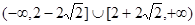
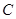 :
: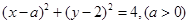 及直线
及直线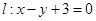 ,当直线
,当直线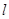 被
被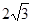 时,则
时,则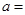 ( )
( )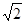 B
B 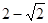 C
C 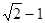 D
D 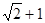
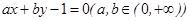 平分圆
平分圆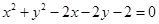 ,则
,则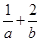 的最小值是( )
的最小值是( )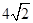
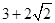
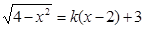 有两个不相等的实根,则实数k的取值范围是( )
有两个不相等的实根,则实数k的取值范围是( )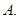
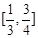
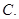

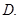
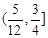
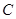 :
: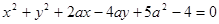 上所有的点均在第四象限内,则实数
上所有的点均在第四象限内,则实数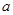 的取值范围为
的取值范围为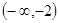
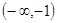
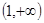
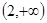
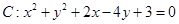 关于
关于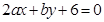 对称,则由点(a,b)向圆C所作切线长的最小值是( )
对称,则由点(a,b)向圆C所作切线长的最小值是( )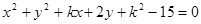 相切,则实数
相切,则实数